Harris' blog

Dans le cadre de mon enseignement aux différents stages ayant trait aux risques radiologiques, les stagiaires (techniciens du CEA, du CERN, du laboratoire central de la préfecture de Paris, militaires du centre de défense NRBC, pompiers professionnels spécialistes NRBC (BSPP, marin pompiers de Marseille etc.)  sont confrontés à des calculs de radioprotection.

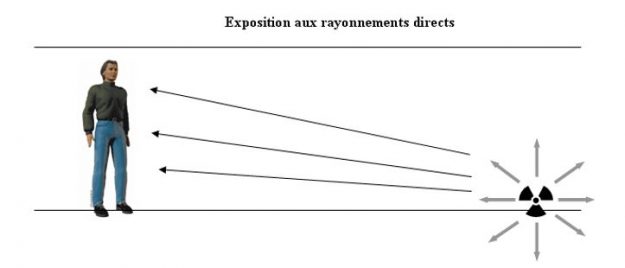
Ces calculs leur permettent de prévoir et donc d’organiser les secours en présence de sources radioactives ponctuelles variées. En fonction de divers paramètres (nature du radioélément, période de radioactivité, activité connue, informations obtenues à partir du guide pratique des radionucléides etc.) ils doivent être en mesure de prévoir les risques d’irradiation de la population et des intervenants et de s’assurer que les valeurs que prévoit la législation ne sont pas dépassées. Sur le terrain, ces calculs sont en général fait “à la louche” en privilégiant les valeurs les plus élevées dans un soucis de sécurité. Mais les apprenants ont également, durant leur formation, à réaliser des calculs précis en rapport avec des exercices de raisonnement tactique qui sanctionnent la réussite (ou l’échec !) à leur stage. Cette fois les résultats se veulent les plus précis possibles. C’est pourquoi il m’a paru nécessaire d’améliorer une méthode de calcul en faisant appel à des outils de mathématiques assez simples qui permettent d’affiner certaines équations.

C’est ce travail que je me permets de vous présenter.

Le postulat de base :

Les rayonnements électromagnétiques X ou γ sont les rayonnements qui intéressent en premier lieu les intervenants. En fonction de leur énergie initiale, ils interagissent avec la matière qu’ils traversent notamment sur les particules du noyau de l’atome : protons et neutrons, ou sur les électrons des couches internes ou externes, (on parle d’« Interactions rayonnements-matière ») principalement par effets photoélectrique pour les basses énergie et la matière traversée de faible numéro atomique, Compton pour des énergies moyennes et production de paires pour des énergie importante.

Lors de l’interaction par effet Compton, un rayonnement électromagnétique diffusé est créé. Nous considérerons ce processus comme défavorable du point de vue de la radioprotection car il s’ajoute au rayonnement initial et augmente le risque d’irradiation.
Pour se protéger, nous utilisons des écrans de matériaux de forts numéros atomiques pour limiter les interactions par effet Compton et favoriser celles par effet photoélectrique moins dangereux.
L’exemple de matériau le plus courant est le plomb (exemples : châteaux de stockage, poubelles blindées, enceintes blindées, etc.). Néanmoins, d’autres matériaux sont utilisés en fonction des applications (l’eau pour son faible coût et sa facilité d’utilisation dans le cas des piscines de stockage dans les centrales nucléaires, les différents bétons pour la construction de casemates. . .).
En règle générale dans la pratique, les écrans doivent être placés aussi près que possible des sources radioactives pour diminuer le poids et le coût de la protection.

• Loi d’atténuation pour un faisceau parallèle mono-énergétique : cas simplifié

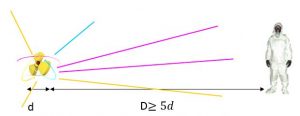
Considérons un faisceau parallèle et mono-énergétique d’un rayonnement électromagnétique traversant normalement un écran d’épaisseur x (dans le cas d’une source ponctuelle, un faisceau parallèle ne peut être généré que si cette source est située infiniment loin de l’écran, sur le terrain il suffit que la distance séparant l’opérateur soit au minimum égale à 5 fois la taille de la source, figure ci-dessous).

Nous savons que connaissant le nombre de rayons incidents N0, nous pouvions écrire :

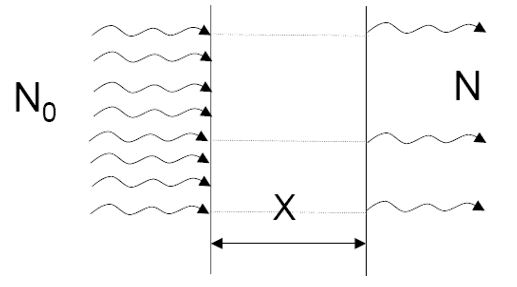
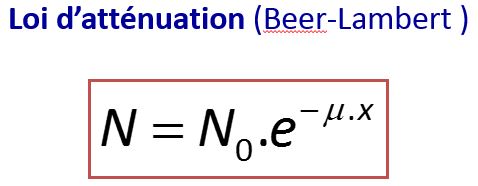
N étant le nombre de rayonnements n’ayant subi aucune interaction dans la traversée de l’écran et μ le coefficient d’atténuation linéique.
De la même manière, si ◦ D0 est le débit de dose absorbée à l’entrée de l’écran et ◦D le débit de dose absorbée à la sortie, dû aux rayons émergents dans la direction initiale avec l’énergie initiale (donc n’ayant pas interagi), alors nous pouvons écrire :

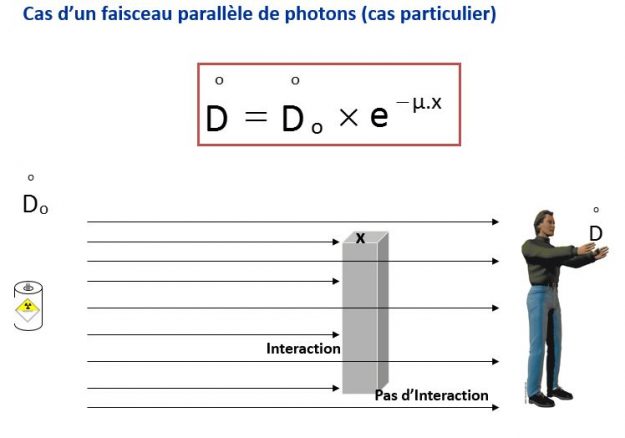
la valeur μ dépend de la nature du matériau constituant l’écran et de l’énergie du rayonnement électromagnétique (μ a les dimensions de l’inverse d’une longueur).

• Loi d’atténuation pour un faisceau parallèle mono-énergétique : cas général

En réalité, seuls les rayonnements ayant interagi dans l’écran par effet photoélectrique sont définitivement arrêtés. L’écran est source de rayonnements diffusés (principalement dus à l’effet Compton), d’énergies inférieures à l’énergie initiale, émis dans des directions diverses, dont une partie contribue à augmenter le débit de dose absorbée en un point quelconque derrière l’écran (Figure ci-dessous). C’est pourquoi la formule précédente donnant l’atténuation doit être corrigée par un facteur multiplicatif supérieur à 1, appelé facteur d’accumulation en dose majoré que l’on note B_D∞ ou « build up factor ».

 

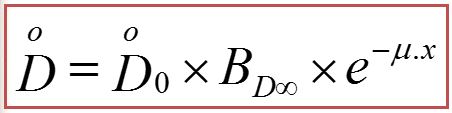
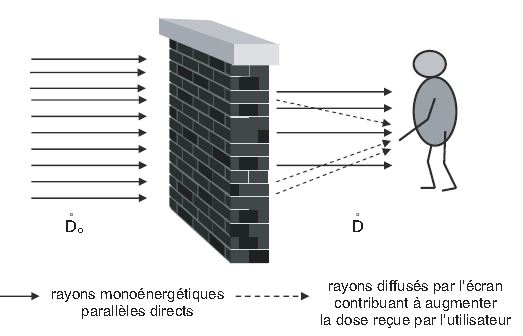
B_D∞ dépend :
– de l’énergie du rayonnement γ (des photons) ;
– de la nature et des dimensions de l’écran ;
– de la situation du point de mesure ;
– de l’environnement.
Le calcul de B_D∞ dans chaque situation particulière est donc infaisable. Nous lui substituerons une valeur majorée, notée  B_D∞ obtenue dans le cas d’un milieu semi-infini, éliminant ainsi les paramètres géométriques.

B_D∞ n’est alors fonction que du produit μx (μ étant le coefficient d’atténuation linéique et x l’épaisseur du mur).

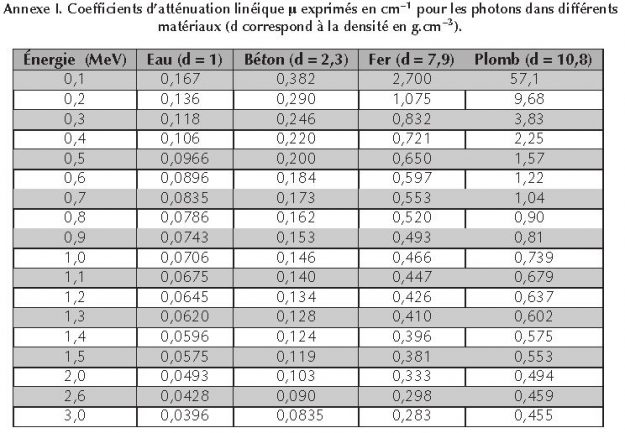
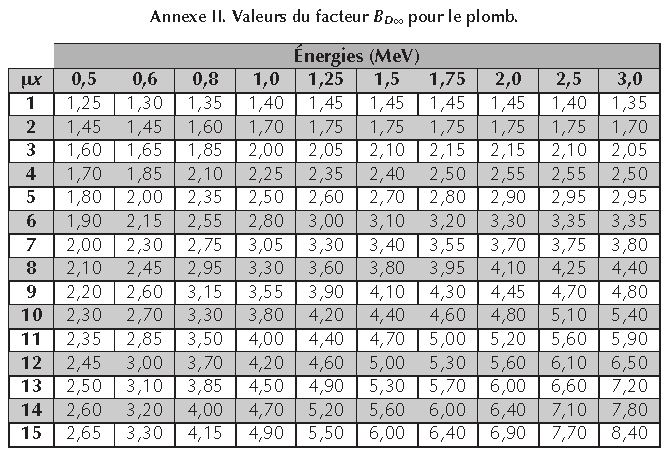
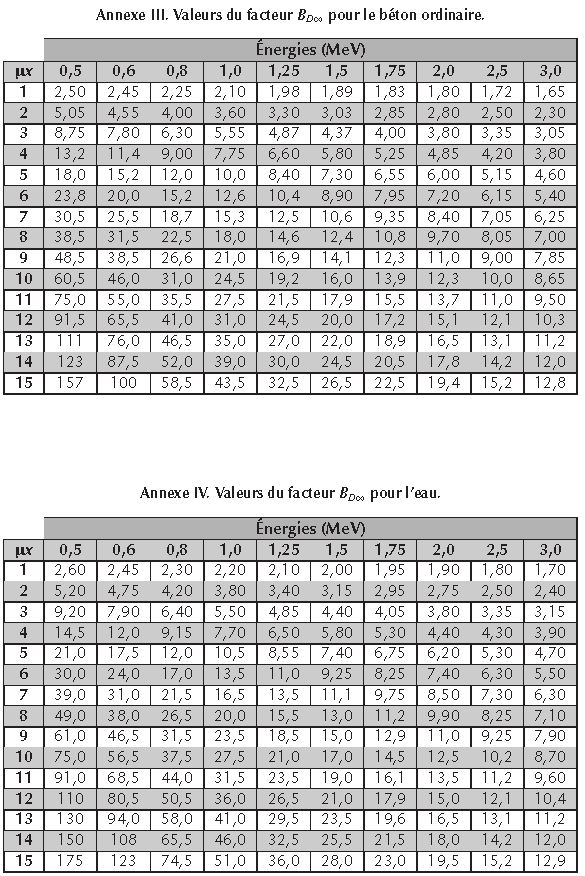
Des tableaux rassemblent les valeurs de μ et de BD∞ respectivement dans le béton, le plomb et l’eau pour différentes valeurs de μx en fonction de l’énergie du rayonnement électromagnétique.

On peut donc en utilisant ces abaques retrouver une valeur approximative de B_D∞ et de μ.

Mon travail a consisté à déterminer quelle pouvait être l’équation mathématique à utiliser pour déterminer la valeur de B_D∞ et de μ de façon beaucoup plus précise.

• En reprenant le tableau permettant le calcul du coefficient d’atténuation linéique ci-dessous,

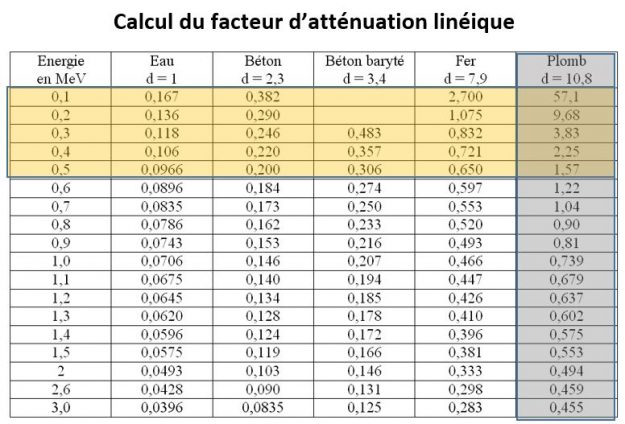
On est capable de tracer une courbe d’interpolation pour le plomb que l’on va considérer comme étant en réalité une succession de segments divers (figure ci-dessous). L’interpolation linéaire est la méthode la plus simple pour estimer la valeur prise par une fonction continue entre deux points déterminés (interpolation). Elle consiste à utiliser pour cela la fonction affine (de la forme f(x) = a.x +b) passant par les deux points déterminés. Cette technique était d’un emploi systématique lorsque l’on ne disposait que de tables numériques pour le calcul avec les fonctions transcendantes : les tables comportaient d’ailleurs à cet effet en marge les « différences tabulaires », auxiliaire de calcul servant à l’interpolation linéaire.

Même si le calcul n’est pas difficile, il est important que la valeur obtenue par interpolation soit déterminée correctement et avec rigueur.

La formule d’interpolation linéaire s’énonce comme suit :

Où :

• A_sup. = Valeur supérieure connue
• A_inf. = Valeur inférieure connue
• B_sup. = Valeur supérieure correspondante
• B_inf. = Valeur inférieure correspondante
• A_int = Valeur intermédiaire connue
• B_int = Valeur intermédiaire correspondante inconnue

On peut également définir l’interpolation linéaire de la façon suivante : Soit f une fonction définie sur R , [a; b] un intervalle de R et c un nombre réel . Quand il n’est pas possible de calculer l’image de c par f , on utilise une interpolation linéaire, cela consiste à remplacer f(c) par g(c) ou g est la fonction affine telle que g(a) = f(a) et g(b) = f(b).

Cela consiste à remplacer la courbe représentative de f sur [a; b] par la droite (AB) ( On dit que l’on a déterminer f(c) par interpolation linéaire.)

Reprenons notre courbe de valeurs :

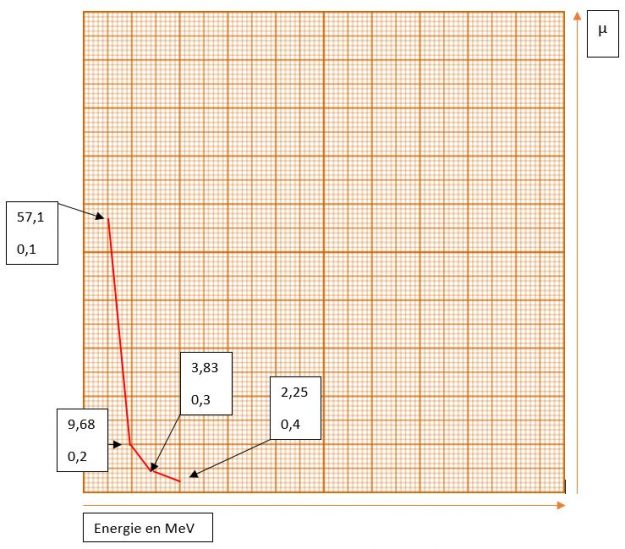
Entre deux points P1 et P2 de coordonnées respectives (E 1 ; μ1) et (E 2 ; μ2), l’interpolation linéaire du point intermédiaire Pi (E i ; μi) est donnée par la formule suivante :

μi = p. (Ei – E 1) + μ1

Avec la pente p qui s’exprime comme :

Ce qui donne en remplaçant P:

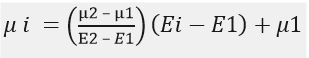
Et par conséquent :

• Concernant le facteur d’accumulation de dose, on procède à l’identique en constatant toutefois que le sens de la pente est différent (pente ascendante)

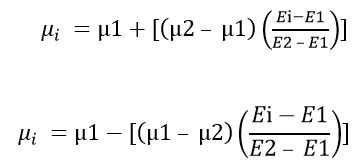
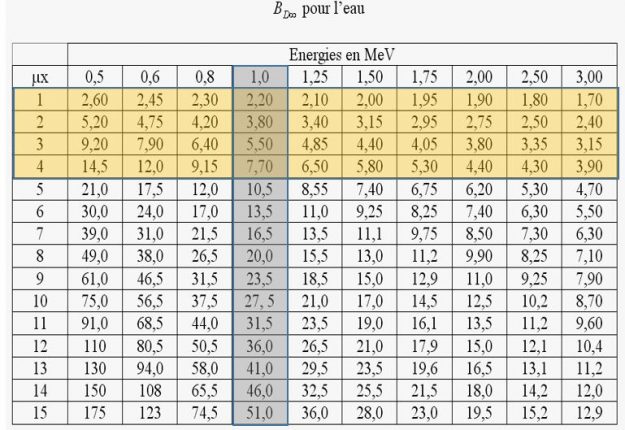
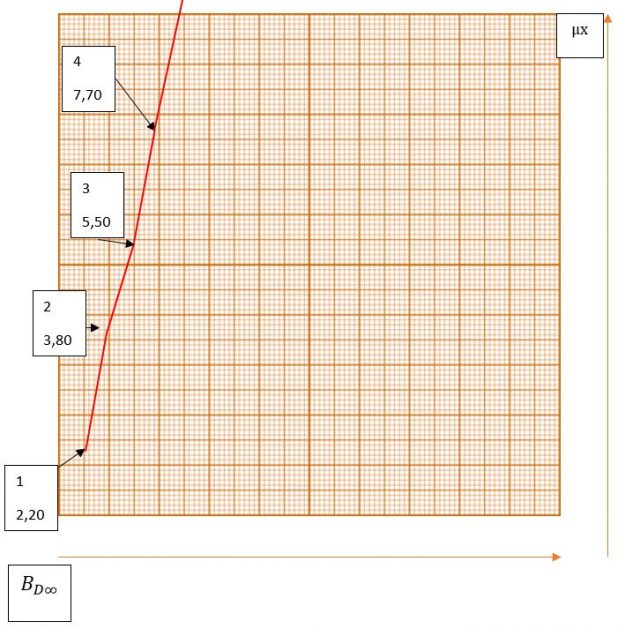
Entre deux points P1 et P2 de coordonnées respectives (μx1 ; B_D∞1 ) et (μx2 ; B_D∞2 ), l’interpolation du point P intermédiaire de coordonnées : (μxi ; B_D∞i ) est donnée par la formule suivante :

B_D∞ i = p. (μxi – μx1) + B_D∞1

Avec la pente p qui s’exprime comme :

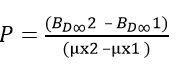
Ce qui donne :

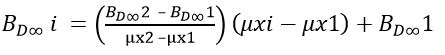
Et par conséquent :

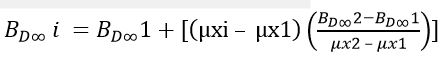
Ainsi, connaissant les valeurs données par les abaques, il est possible de calculer de façon précise les valeurs intermédiaires tant du coefficient d’atténuation linéique que du facteur d’accumulation de dose.

Les phénomènes de diffusion dans l’écran ne sont pas à négliger et il est toujours préférable d’en tenir compte pour effectuer ce genre de calcul de radioprotection.

 

ANNEXES

(D’après Radiation dosimetry, Attix F., Roesch W., Academic Press, 1968.)

Bibliographie

 

• Jean Laborde (préf. de Jean Kuntzmann), Tables numériques de fonctions élémentaires, éd. Dunod, 1961 (rééd. 1968, 1976) – 149 pages
• André Delachet, Les logarithmes, Presses Universitaires de France, coll. « Que sais-je ? », 1960 (réimpr. 1964, 1968, 1972, 1977), 128 p., « Le calcul logarithmique », p. 47-80