


Retrouvez ici même, des énigmes amusantes, pour tous les âges et tous les niveaux jusqu’en terminale S, qui vous feront réfléchir et passer un peu de temps. N’allez pas chercher les solutions sur internet, vous risquez d’être désagréablement surpris, les solutions sont parfois fausses ou tout simplement incompréhensibles…
Ici, il n’y a rien à gagner, ni de classement des meilleurs esprits, l’intérêt est de simplement faire travailler ses neurones.
Je place également EN FIN DE PAGE les solutions que j’ai trouvées personnellement et qui ne sont peut être pas les plus simples ou les plus évidentes pour vous. N’hésitez pas à me faire remonter vos remarques.
Si vous avez des énigmes sympas que je ne connais pas, n’hésitez pas à me les soumettre.
Sur la page, les énigmes vont de la plus récente à la plus ancienne !
Et comme je le dis régulièrement à mes élèves de mathématiques:
Bien lire le texte est nécessaire pour traiter ce type de problèmes.
Les hypothèses données peuvent vous indiquer la méthode à utiliser.
Bien choisir les inconnues. Il faut éviter d’en oublier ou même d’en rajouter d’inutiles.
Mal traduire les hypothèses et surtout en oublier est une cause d’erreur ou d’impasse possible.
Ne vous laissez pas impressionner par un texte qui peut paraître compliqué.
Dans ce type de problèmes, il y a souvent des informations qui ne servent pas forcément pour la résolution.
Ne pas oublier des informations non écrites mais qui sont liées à la nature du problème.
Une distance est un nombre positif ; Un nombre d’objet est un nombre entier ;
Tous les animaux n’ont pas le même nombre de pattes.
Si le problème a un support géométrique, ne pas faire de figure est une source supplémentaire de difficultés.
Souvent la figure est, en soi, un début de piste.
ENIGME N° 28: (Solution plus bas)
ENIGME N° 27: (Solution plus bas)
Un père promet à son fils de lui offrir 5€ pour chaque bonne réponse mais le fiston devra lui donner 8€ à chaque mauvaise réponse.
Au bout de 26 questions, le père et le fils ne se doivent rien.
Combien le fils a-t-il donné de bonnes réponses ?
ENIGME N° 26: (Solution plus bas)
J’achète un tableau 40000€, je le revends 60000€.
Puis je le rachète 80000€ pour le revendre à 100000€.
Combien ai-je gagné ?
ENIGME N° 25: (Solution plus bas)
En se rendant à un point d’eau, un zèbre croise 6 girafes qui s’y rendaient également.
Chaque girafe portait sur son dos 3 singes.
Chaque singe portait 2 oiseaux qui eux-mêmes portaient chacun 4 mouches.
Combien d’animaux au total se retrouvent au point d’eau ?
ENIGME 24:(Solution plus bas)
Il faut 1min25s pour couper une bûche en deux.
Combien de temps faut-il pour couper une bûche en 13 morceaux ?
ENIGME 23:(Solution plus bas)
Quatre tapissiers font 4 tapis en 4 jours.
Combien faut-il de tapissiers pour faire 20 tapis en vingt jours ?
ENIGME 22:(Solution plus bas)
Un mathématicien dit à son facteur:
“J’ai trois filles. Le produit de leurs âges est égal à 36 et la somme de leurs âges égale le numéro de la maison située en face de la mienne. Pouvez-vous me donner leurs âges ?”
Le facteur réfléchit puis répond: “Mais il me manque une donnée !”
Le mathématicien rajoute alors:
“En effet, l’aînée s’appelle Charlotte.”
Le Facteur donne la réponse. Quelle est-elle ?
ENIGME 21: (Solution plus bas)
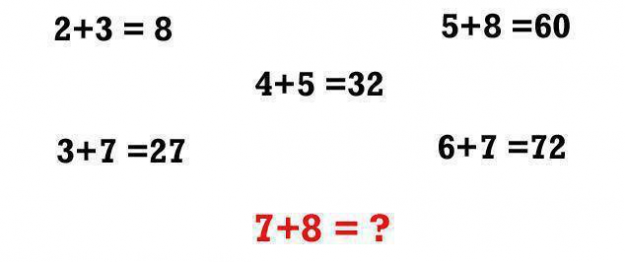
ENIGME 20: (Solution plus bas)
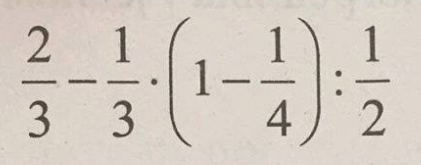
ENIGME 19: (Solution plus bas)

ENIGME 18
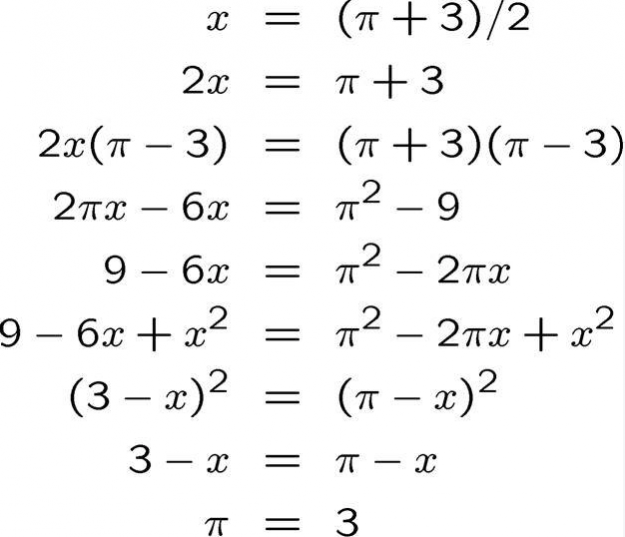
ÉNIGME N°17 (correction plus bas)
Deux trains, séparés de 200 km roulent l’un vers l’autre. Chacun avance à 50 km/h.
Une mouche part de l’avant de l’un d’eux et vole à la vitesse de 75 km/h jusqu’à ce qu’elle rencontre le second train. A ce moment-là, elle fait demi-tour, jusqu’à ce qu’elle rencontre le premier train, puis fait demi-tour jusqu’à ce qu’elle rencontre le second et ainsi de suite, jusqu’à ce que les trains la tuent en se croisant.
Quelle distance totale la mouche a-t-elle parcouru pendant ce vol ?
ÉNIGME N°16 (correction plus bas)

Il y a des porcs et des oies derrière la maison. On voit 72 têtes et 200 pieds. Combien y a-t-il de porcs ?
ÉNIGME N°15 (correction plus bas)
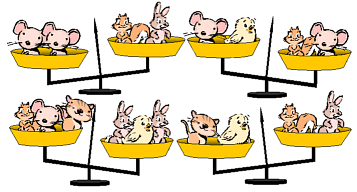
Mary adore les peluches. Elle en a même plusieurs en double. Mais compte tenu des indications du dessin, pourriez-vous les classer de la plus légère à la plus lourde ?
ÉNIGME N°14 (correction plus bas)
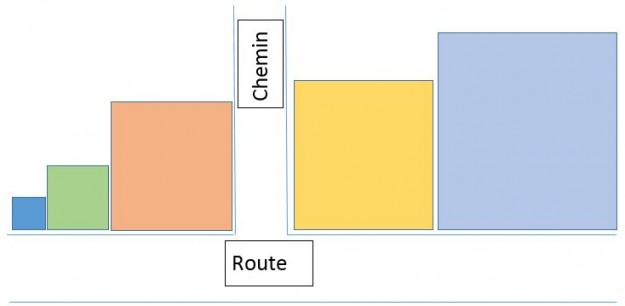
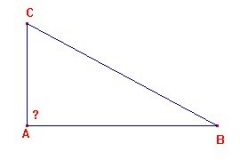
Deux frères ont hérité de 5 terrains carrés dont les côtés ont pour longueur cinq nombre entiers consécutifs.
Les terrains sont disposés en deux groupes le long d’une route : les trois “plus petits” d’un côté d’un chemin et les deux “plus grands” de l’autre côté du chemin.
Déterminer les dimensions des terrains telles que les aires de part et d’autre du chemin soient égales.
ÉNIGME N°13 (correction plus bas)

ÉNIGME N°12 (correction plus bas)

L’herbe d’un pré pousse partout avec même vitesse et la même densité. On sait que 70 vaches la mangent en 24 jours alors que 30 vaches la mangent en 60 jours.
Combien faudrait-il mettre de vaches dans le pré pour qu’elles mangent l’herbe en 96 jours?
ÉNIGME N°11 (correction plus bas)

Quand Timothée aura l’âge qu’a maintenant son père, alors sa sœur sera deux fois plus vieille.
D’autre part, l’âge du père sera le double de l’âge de Timothée quand sa sœur aura l’âge actuel de son père. En outre, la somme de leurs âges est d’un siècle. Mais quel est l’âge de chacun?
ÉNIGME N°10 (correction plus bas)

Une épigramme grecque, publiée vers 369 dans L’Abrégé de l’Histoire Romaine d’Eutrope, propose de calculer l’âge de Diophante. Voici la traduction en alexandrins qu’en donne Emile Fourrey dans ses Récréations mathématiques.
Passant sous ce tombeau repose Diophante.
Ces quelques vers tracés par une main savante
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s’écoula,
Puis s’étant marié, sa femme lui donna
Cinq ans après un fils, qui, du destin sévère,
Reçut de jours hélas! deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, si tu sais compter, à quel âge il mourut.
Saurez-vous calculer l’âge de Diophante?
ÉNIGME N°9 (correction plus bas)

L’océan Atlantique fait la moitié du Pacifique.
L’Arctique fait le quart de l’Atlantique.
L’Arctique et l’Antarctique font ensemble les deux cinquièmes de l’océan Indien, qui fait lui-même fait les neuf dixièmes de l’Atlantique.
Mais alors, combien faut-il d’océans Antarctique pour recouvrir tout le Pacifique?
ÉNIGME N°8 (correction plus bas)

J’ai toujours mal quelque part!
Un jour sur trois, j’ai mal au dos! Un jour sur quatre, j’ai mal aux dents! Un jour sur cinq, j’ai la migraine!
Et même, un jour sur six, je souffre de deux de ces maux!
Mais, le pire, c’est les jours maudits, où j’ai mal au dos, aux dents, et à la tête…
Au fait, quelle est leur fréquence?
ÉNIGME N°7 (correction plus bas)

5 chameaux boivent 5 bonbonnes d’eau en 5 jours.
7 dromadaires boivent 7 bonbonnes d’eau en 7 jours.
Mais qui boit le plus? Un chameau ou un dromadaire?
ÉNIGME N°6 (correction plus bas)

Avec 10 bougies brûlées, vous fabriquez 1 bougie neuve.
Combien de bougies aurez-vous fabriquez avec 1000 bougies ?
ÉNIGME N°5 (correction plus bas)
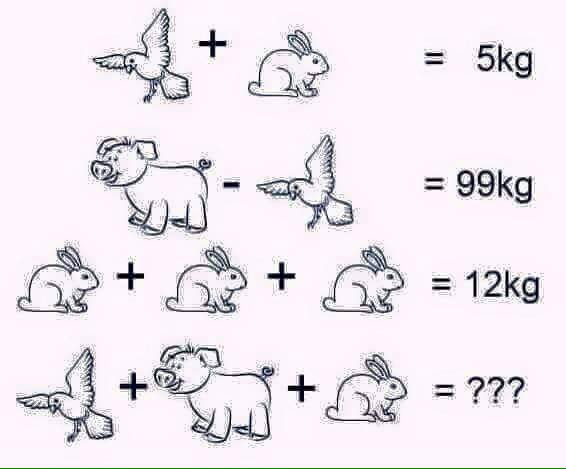
ÉNIGME N°4 (correction plus bas)

ÉNIGME N°3 (correction plus bas)
Résoudre :
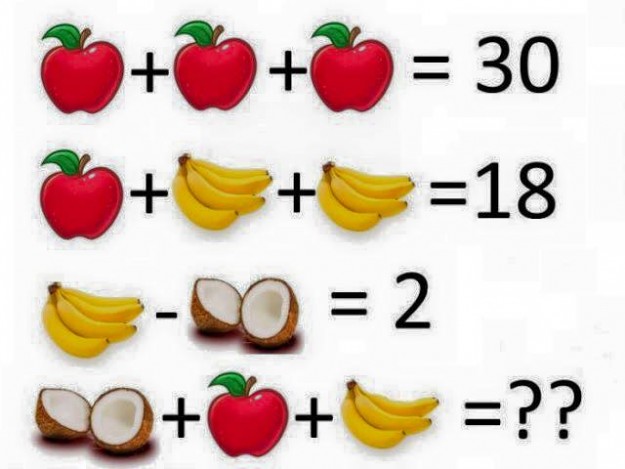
ÉNIGME N°2 (correction plus bas)

ÉNIGME N°1 (correction plus bas)
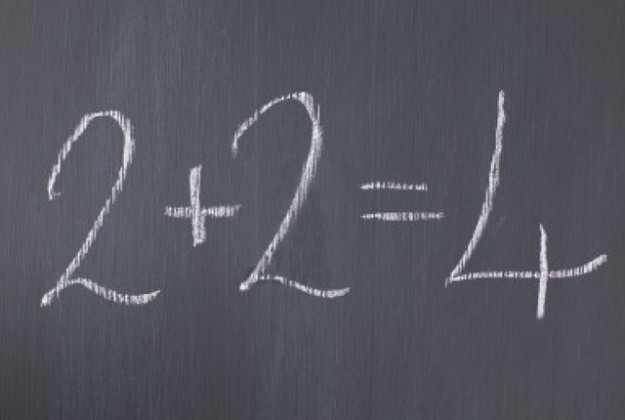
Quelle est la moitié de 2 + 2 ?
Si vous trouvez 2, c’est une erreur !
SOLUTIONS DES ÉNIGMES
N°28
N°27
Soit x le nombre de bonnes réponses et y le nombre de mauvaises réponses.
Il y a 26 questions, donc : x + y = 26, soit y = 26 – x.
Le père donne a son fils 5€ par bonne réponse. Il donne en tout 5x euros.
Le fils lui rend 8€ par mauvaise réponse. Le fils donne en tout 8y euros.
A la fin, le père et le fils ne se doivent rien, donc : 5x = 8y.
En remplaçant y = 26 – x dans cette nouvelle équation, on obtient : 5x = 8(26 – x), soit :
5x = 208 – 8x
5x + 8x = 208
13x = 208
x = 208/13 = 16
Le fils a donc donné 16 bonnes réponses.
N°26
Deux bénéfices de 20 000€ font 40 000€.
N°25
205 animaux se trouvent au point d’eau.
En détail, cela donne : 1 zèbre + 6 girafes + 18 (3×6) singes + 36 (2×18) oiseaux + 144 (4×36) mouches.
N°24
Pour couper une bûche en 13 morceaux, il faut faire 12 coupes prenant chacune 1min25s, soit : 12 x 1min25s = 17min.
N°23
Si 4 tapissiers font 4 tapis en 4 jours,
alors 4 tapissiers font 4×5 tapis en 4×5 jours.
La réponse est donc 4 tapissiers.
Il y a proportionnalité entre le nombre de tapis et le nombre jours.
N°22
Le produit de leurs âges est = 36.
Décomposons 36 de façon à envisager toutes les solutions :
36 = 1 x 1 x 36
36 = 1 x 2 x 18
36 = 1 x 3 x 12
36 = 1 x 4 x 9
36 = 1 x 6 x 6
36 = 2 x 2 x 9
36 = 2 x 3 x 6
36 = 3 x 3 x 4
On a pour le moment 8 possibilités. Additionnons les âges.
1 + 1 + 36 = 38
1 + 2 + 18 = 21
1 + 3 + 12 = 16
1 + 4 + 9 = 14
1 + 6 + 6 = 13
2 + 2 + 9 = 13
2 + 3 + 6 = 11
3 + 3 + 4 = 10
Le facteur voit le numéro de la maison située en face de celle du mathématicien donc, comme il lui manque un indice, ce numéro est le 13 (c’est le seul numéro présent deux fois) et le facteur hésite entre :
1 an, 6 ans et 6 ans avec deux ainées jumelles,
2 ans, 2 ans et 9 ans.
L’aînée s’appelle Charlotte et est unique, la solution est : 2 ans, 2 ans et 9 ans.
N° 21
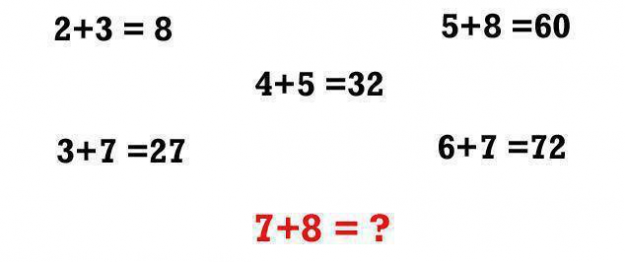
Pour cette énigme, il faut pas mal d’observation, un bon sens du classement, un peu de logique, une bonne connaissance des tables de multiplications et un peu de tâtonnement comme souvent en mathématiques.
Classons les équations de façon à ce que le premier terme de l’addition fasse une suite numérique croissante :
2 + 3 =8
3 + 7 = 27
4 + 5 = 32
5 + 8 = 60
6 + 7 = 72
7 + 8 = ?
On a bien 2, 3, 4, 5, 6, et 7.
En observant les termes à droite du signe =, on constate que tous les nombres sont des produits d’un nombre entier avec le premier terme de chaque addition. Exemple : 8 = 2 x 4 avec 2 le premier terme de 2 + 3 = 8. Il reste à trouver une forme d’algorithme qui permet de trouver 4 en manipulant 2 et 3 simplement, puis de comparer cet algorithme avec les propositions suivantes.
CQFD
N°20
Dans cette énigme, il est impératif de se souvenir des règles de priorité dans les calculs simples avec les opérations courantes. Que précisent ces règles ?
Donc : 2/3 – 1/3 . (3/4) : 1/2 = 2/3 – 1/4 x 2 = 2/3 – 1/2 = 4/6 – 3/6 = 1/6
CQFD
N°19
On sait que 7 personnes ont un ordinateur et un téléphone allumés.
On en déduit que :
On sait aussi que 9 personnes n’ont aucun appareil allumé
Donc : 7 + 8 + 6 + 9 = 30 passagers (hors équipage)
CQFD
N° 18
N°17
L’erreur ici serait d’imaginer les aller-retours incessants que va faire notre mouche entre les deux trains. Il faut simplement ne pas se mettre à la place de la mouche, mais à la place des trains. C’est une erreur que font environ 99 % des personnes qui tentent de résoudre cette énigme. Et la solution des problèmes de maths vient très souvent d’un changement de place de l’observateur. Je m’explique:
Les trains vont l’un vers l’autre à la même vitesse et partent au même moment. Lorsqu’ils se croiseront ils auront parcouru la même distance soit la 1/2 de 200 Kms = 100 Kms. Comme ils roulent à 50 Km/h, ils auront roulé 2 heures avant de se croiser et de tuer la mouche.
Avant de se faire écraser, notre copine la mouche aura donc volé durant 2 heures. Sa vitesse étant de 75 Km/h, elle aura parcouru 150 Kms… CQFD
N° 16
Il s’agit d’un système de deux équations à deux inconnues.
Soit x le nombre de cochons et y le nombre d’oies.
On a 72 têtes d’animaux soit : x + y = 72 donc x = 72 – y
on a 2 pattes pour les oies donc : 2y en nombre de pattes
on a 4 pattes pour les cochons donc : 4x en nombre de pattes, ce qui fait : 2x + 4y = 200
On remplace x par sa valeur (72 – y) et on obtient : 2(72 – y) + 4y = 200 d’où on extrait y = 28 cochons… CQFD
N°15
Traduisons le dessin sous la forme d’inéquations. Soit C la masse du chat, E celle de l’écureuil, S celle de la souris, P celle du poussin et L celle du lapin…
On obtient :
1) S + S > E + L
2) S + E > S + P
3) L + L + P > E + S + C
4) C + P > E + L
D’après 2), S + E > S + P donc E > P.
L’écureuil est plus lourd que le poussin.
D’après 4), C + P > E + L, et comme E > P, C + P > E + L > P + L, soit C > L.
Le chat est plus lourd que le lapin.
D’après 3), L + L + P > E + S + C ; et comme C > L,
C + L + P > L + L + P > E + S + C, soit L + P > E + S.
Puisque L + P > E + S et que E > P, L + E > L + P > E + S, soit L > S.
Le lapin est donc plus lourd que la souris.
D’après 1), S + S > E + L. Et comme L > S, L + S > S + S > E + L, soit S > E.
Donc la souris est plus lourde que l’écureuil.
Ce qui donne, par ordre croissant,
Poussin < Ecureuil < Souris < Lapin < Chat… CQFD
N°14
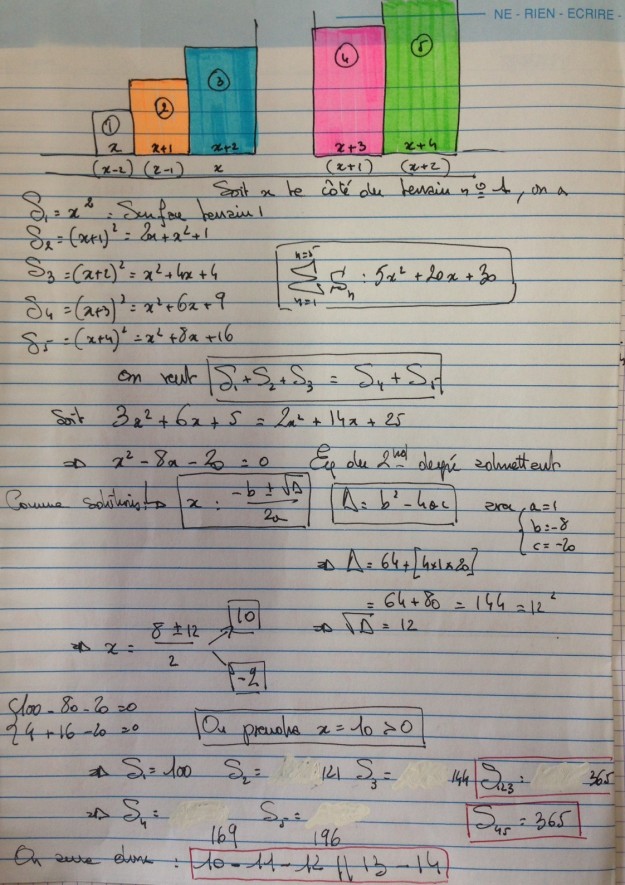
N°13
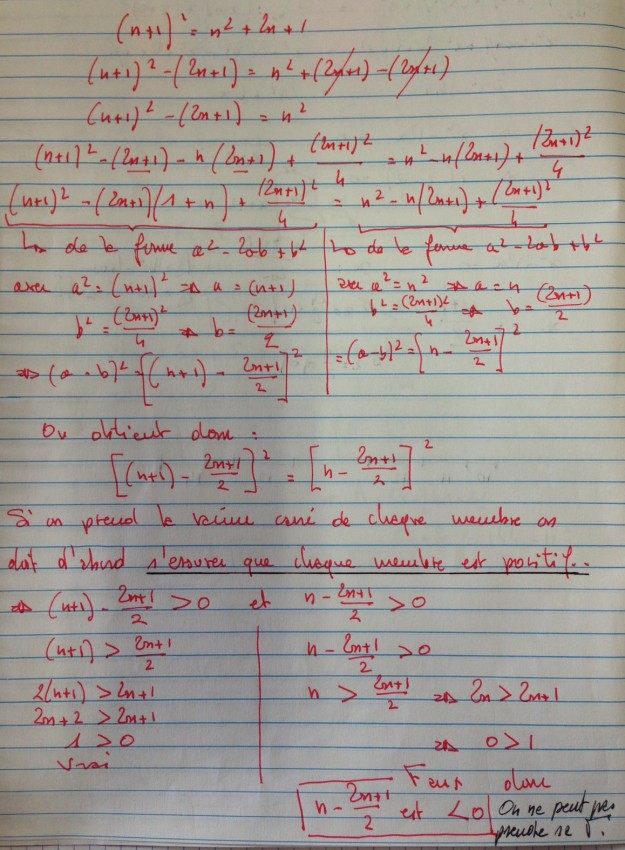
N°12
Notons
Le problème nous donne les informations suivantes :

On souhaite trouver n qui est donné par :

A première vue, cela a l’air impossible, car on a trois inconnues (x,y et K) et seulement deux équations pour les déterminer. Mais en fait, ce qui nous intéresse vraiment, ce sont les valeurs de y/x et K/x. En effet, n est donné par la relation :

Mais le système initial se réécrit en :

Il est alors facile d’obtenir y/x = 10/3, K/x = 1600 et n = 20. Il faut donc 20 vaches pour brouter le pré en 96 jours! CQFD
N°11
On va se ramener à un système d’équation à 3 inconnues.
On notera x,y,z les âges respectifs de Timothée, de sa sœur, et de son père. La première équation, est facile à obtenir : puisque la somme des âges est égale à une siècle, on a
Analysons les autres phrases :
Remarquons que les deux équations nous donnent immédiatement que z = 50.
On résoud le système, en ayant déjà remarqué que z = 50. Il vient y = 50 − x et y = 2x, soit 100 = 3x, soit x = 50/3, et donc y = 100/3. CQFD
N°10
Notons x l’âge de Diophante. Les diverses informations données par le poème conduisent à l’équation suivante :
On obtient facilement la solution : x=84. CQFD
N°9
L’océan ‘indien fait les 9/20 du Pacifique, et donc Arctique et Antarctique ensemble font 18/100=9/50 du Pacifique.
Mais l’Arctique seul fait 1/4×1/2=1/8 du Pacifique. L’Antarctique fait donc 9/50-1/8=11/200 du Pacifique.
Il faut donc 200/11, soit un peu plus de 18, océans de la taille de l’Antarctique pour recouvrir tout le Pacifique. CQFD
N°8
C’est un simple calcul de fractions!
Soit f la fréquence où j’ai mal aux 3 endroits.
On a : 1=f+1/3+1/4+1/5+1/6.
D’où, en réduisant tout au même dénominateur, on a f=3/60=1/20 :
j’ai donc mal au dos, aux dents et à la tête un jour sur 20 ! CQFD
N°7
Un chameau boit un cinquième de bonbonne d’eau par jour, et un dromadaire boit un septième de bonbonne d’eau par jour. Les chameaux boivent donc beaucoup plus que les dromadaires! CQFD
N°6
Nous avons affaire à un outil particulier des mathématiques qui s’appelle le “calcul récursif”, méthode très utilisée en informatique. Détaillons le problème.
Nous savons que 10 bougies brûlées servent à produire 1 bougie. On nous en propose 1000. Avec ces 1000 on va fabriquer 100 bougies qui vont également servir à fabriquer 10 bougies avec lesquelles je fabriquerai 1 bougie. On constate alors que j’aurai bien fabriqué : 100 + 10 + 1 bougies, soit 111 bougies. CQFD
N°5
A peu près le même exercice qu’avec les pommes, les bananes et les noix de coco. Ici encore la possibilité de passer par un système d’équation du premier ordre. Définissons les inconnues. P = Pigeon, L = Lapin, C = Cochon.
Connaissant L, on en déduit de la ligne 1, P = 5 – L = 5 – 4 = 1
Connaissant P, on en déduit de la ligne 2, C = 99 + P, C = 99 + 1 = 100
En final on obtient : P + C + L = 1 + 100 + 4 = 105 CQFD
N°4
La démonstration présentée parait tellement exacte qu’il est parfois difficile de trouver l’erreur et je reste persuadé que si l’on ne dit pas qu’il y a une erreur, on ressort convaincu de la véracité de la démonstration. C’est un peu le piège des mathématiques.
Jusqu’à la 7ème ligne tout est juste. On se retrouve avec 2 (a²-ab) = 1 (a² – ab), que l’on va simplifier en divisant chacun des membres à gauche comme à droite par (a² – ab) et finir par trouver (pour ne pas dire prouver) que 2 = 1 !
C’est ici qu’apparaît l’erreur impardonnable 😉 ! Lorsque on utilise un dénominateur constitué de valeurs supposées connues (des paramètres) il est impératif de s’assurer que ce dénominateur n’est pas égal à 0, auquel cas la division est tout simplement impossible.
Or, que nous dit-on en première ligne ? a = b. Par conséquent a x a = a² est égal à ab ce qui implique que a² – ab est = 0.
On n’a dons pas le droit de diviser par (a² – ab) puisque cet élément est nul.
C’est ici que se situait l’erreur de la démonstration ! CQFD
N°3
Pour cette énigme, il faut un bon sens de l’observation et ne pas se jeter comme un fou sur une solution qui parait sauter aux yeux. Prendre son temps pour analyser le problème c’est 80% de la résolution de l’exercice.
Nous sommes dans un cas typique de résolution d’équations du premier ordre sous forme de système. il faut définir les inconnues. Prenons P pour les pommes, B pour les bananes, et C pour la noix de coco.
N°2
Pour ce problème, pas besoin de passer par la notion de changement de base de calcul. c’est plus simple.
Voici ma façon de résoudre ce problème:
L’alphabet compte 26 lettres. On peut donc remarquer que l’on va changer de 1ère lettre toutes les 26 souris. En partant de AA la 26ème souris sera nommée AZ, la 52ème (2×26) souris sera BZ, la 78ème (3×26) se nommera CZ et ainsi de suite.
Si je divise 500 par 26, je trouve 19, reste 6. J’ai donc en réalité 19 x 26 = 494 et qui correspond à ma 494ème souris. elle se nommera SZ puisque S est la 19ème lettre de l’alphabet. La 495ème souris se nommera TA, la 496ème TB, la 497ème TC, la 48ème TD, la 499ème TE…
et la 500ème TF ! CQFD
N°1
Dans cette énigme, il est impératif de se souvenir des règles de priorité dans les calculs simples avec les opérations courantes. Que précisent ces règles ?
On nous dit : Quelle est la moitié de 2 + 2 ? dans cet exercice il faut comprendre, (quelle est la moitié de 2) + 2, ainsi on trouve : (2/2) + 2 = 1 + 2 = 3
Il s’agit juste d’un problème de lecture correcte de l’énoncé. CQFD