Harris' blog

« Que j’aime à faire apprendre un nombre utile aux sages !

Immortel Archimède , artiste , ingénieux ,              

Qui de ton jugement peut priser ta valeur ?

Pour moi, ton problème eut de pareils avantages ! »

Le nombre pi est connu depuis l’antiquité, évidemment, pas au sens où nous l’entendons maintenant (notion abstraite de constante mathématique) mais en tant que rapport entre la longueur du cercle et son diamètre et d’ailleurs surtout en tant que méthode de calcul du périmètre du cercle (ou de l’aire du disque). Disons-le tout net, sans le nombre π, il n’y aurait pas de table ronde, de roue qui roule, pas de pleine lune, pas de 2πr ni de πr², pas de problèmes insolubles… et bien d’autres choses encore. l’histoire de π est aussi longue que la liste des nombres qui le composent.

En 2000 av. JC, les Babyloniens connaissaient π (comme le rapport constant entre la circonférence d’un cercle et son diamètre, mais pas comme objet mathématique). Ils avaient comme valeur 3 + 7/60 + 30/3600 (ils comptaient en base 60) soit 3 + 1/8 = 3,125.

Vers 1650 av.JC, les Egyptiens avaient comme valeur (16/9)2 qui vaut environ 3,16. Cette valeur a été retrouvée sur le fameux papyrus de Rhind, écrit par le scribe Ahmès, acheté par un Ecossais qui s’appelle … Henry Rhind. Il est conservé au British museum.

Le Papyrus de Rhind provient du temple mortuaire de Ramsès II à Thèbes, en Egypte (la ville où est érigé le temple de Karnak) et fut acheté par Alexander Rhind. Il a été écrit vers -1650 par le scribe Ahmès. Constitué de 14 feuilles de papyrus, il mesurait à l’origine plus de 5 m de longueur sur 32 cm de large. Il est le plus vieux traité de mathématiques du monde et contient 87 problèmes dont, par exemple, la décomposition des fractions en fractions unitaires (dont le numérateur est 1), de l’arithmétique (multiplications et divisions), résolution d’équations, l’arpentage (mesures des distances) et à la géométrie : aires planes (du trapèze en particulier), volumes de greniers à grains, calcul de pyramides .

Ensuite, π apparaît :

• En Chine vers 1200 av. JC, avec pour valeur 3.
• Dans la Bible vers 550 av. JC, avec pour valeur 3.
• En Grèce, avec en particulier Archimède en 250 av. JC qui donne l’encadrement 223/71 < pi < 22/7 et Ptolémée en 150 qui utilise 3 +8/60 + 30/3600 = 3,1416666.
• En Chine au Vème siècle, avec pour valeur 355/113 = 3,14159292.
• En Inde : 3 + 177/1250 = 3,1416 en 380 puis 3,16227 (racine carrée de 10) avec Brahmagupta en 640
• Au Moyen-Orient avec Al Khwarizmi en 800 (Ouzbekistan) et Al Kashi, professeur de mathématiques et d’astronomie en 1429 (Turkestan) qui calcule 14 décimales de pi. C’est un homme sain d’esprit qui fait des mathématiques partout et tout le temps. C’est en s’intéressant aux propriétés du cercle (des pièces de monnaie que lui rendait un épicier) qu’il fait le rapport entre son diaètre et son périmètre et trouve ainsi π=3,141 ou 3,142, ça dépend ! En effet lorsqu’il calcule la surface de la lune et qu’il divise le résultat par le rayon au carré, il trouve π=3,142. Le mois d’après, il refait son calcul et là, surprise ! il trouve π=3,141. Alors il décide de placer le cercle dans un carré, puis de dessiner un carré à l’intérieur du cercle !

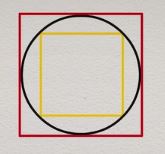
Il en déduite alors l’encadrement de π :

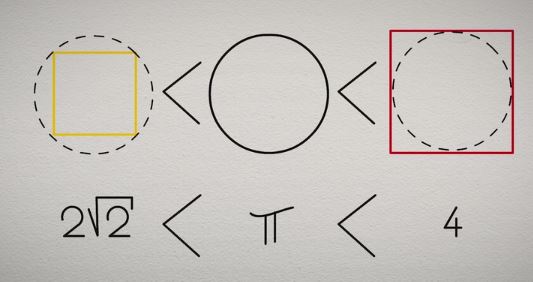
Et par conséquent :

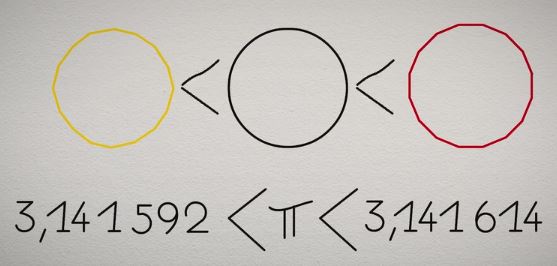
Et voilà ! Al Kashi a enfin pu se rapprocher de la véritable valeur de π.

• En Europe : l’Italien Fibonacci, en 1220, trouve la valeur 3,141818, au Pays-Bas avec Van Ceulen (20 décimales en 1596 puis 34 décimales en 1609 !), en France avec Viète (9 décimales en 1593).

Puis vint le développement des techniques de calculs avec l’analyse (dérivée, intégrales, sommes de séries, produits infinis …), Wallis en 1655, Newton (16 décimales en 1665), Gregory, Leibniz, John Machin (100 décimales en 1706), puis Euler (20 décimales calculées en une heure !) vers 1760 et beaucoup d’autres.

Les champions contemporains sont les frères Chudnovsky avec 4 milliards de décimales en 1994 et Kanada et Tamura dont le dernier record datait de 1999 avec 206 milliards de décimales (en environ 33 heures de calculs). Kanada a battu son propre record le 6 décembre 2002 avec une équipe de neuf autres chercheurs japonais du Information Technology Center de l’Université de Tokyo : 1 241 100 000 000 décimales ont été calculées à l’aide d’un super calculateur Hitachi (400 heures de calculs !) en utilisant un algorithme que l’équipe a mis cinq ans à mettre au point.

En réalité, toutes ces décimales ne servent à rien. En effet pour calculer la surface d’un cercle, ou sa circonférence, 4 ou 5 décimales suffisent !

En mathématiques parfois le résultat est moins intéressant que ce que l’on débusque sur son chemin… π a vu émerger de nombreuses questions et de drôles de réponses.

Les premiers calculs de décimales du nombre π

Les chiffres de π peuvent se retrouver en comptant le nombre de lettres dans le texte ci-dessous :

« Que j’aime à faire apprendre un nombre utile aux sages !

3   1   4        1   5             9                2         6              5     3       5

Immortel Archimède , artiste , ingénieux ,

8                 9                        7                 9

Qui de ton jugement peut priser ta valeur ?

3     2       3         8                 4         6     2         5

Pour moi, ton problème eut de pareils avantages ! »

4        3       3           8             3      2        7                 9

C’est Archimède (né en 287 av. JC à Syracuse et mort en 212 av. JC), en 250 av.JC qui a réellement commencé à calculer des décimales du nombre π. Il est surtout le premier à avoir utilisé un algorithme pour le calcul. La méthode, qu’on appelle naturellement aujourd’hui la méthode d’Archimède, consiste à calculer le périmètre de polygones réguliers inscrits et circonscrits au cercle pour encadrer le périmètre du cercle et donc en déduire un encadrement de π. Il obtint ainsi

3+10/71 < pi < 3+1/7

La notation π est la première lettre du mot grec perimetron, périmètre ou perijereia, circonférence, périphérie.

Il y a plusieurs versions sur l’apparition du symbole, mais l’époque est toujours la même : vers 1600. William Oughtred (1574-1660) en 1647 et Isaac Barrow (1630-1677) utilisent le symbole π pour représenter le périmètre d’un cercle de diamètre 1. Un Allemand, Ludolph von Ceulen (1539-1610) utilisait déjà cette notation. Qui fut le premier ? Est-ce bien important ? Il serait néanmoins intéressant de savoir si ces personnes communiquaient et comment l’usage du symbole π s’est répandu.

En 1706, Jones l’utilise pour désigner le rapport de la circonférence d’un cercle à son diamètre (à cette époque , Bernoulli emploie la lettre c)

Euler , utilise la lettre π ,dans un ouvrage sur les séries, publié en latin en 1737 puis, en 1748, dans son ’’Introduction à l’analyse infinitésimale’’, ce qui imposa définitivement cette notation .
Nature algébrique de π.

π n’est pas un nombre décimal, c’est-à-dire que les chiffres après la virgule ne sont pas en nombre fini (pi a une infinité de décimales). La meilleure valeur décimale approchée de π connue actuellement comporte environ 1241 milliards de chiffres … Autant dire presque rien !

π est un nombre irrationnel, c’est-à-dire qu’il ne peut pas s’écrire comme une fraction de deux nombres entiers. Autrement dit, cela signifie aussi que les chiffres de π ne sont pas prévisibles. On ne peut pas deviner une décimale sans la calculer explicitement, comme on peut le faire par exemple avec le nombre 1/7 = 0,14285714285714.
L’irrationalité de π fut démontrée en 1761 par l’Allemand Lambert.

π est un nombre transcendant c’est-à-dire qu’il n’est solution d’aucune équation à coefficients rationnels. Cela fut démontré en 1881 par Lindemann.
La quadrature du cercle.

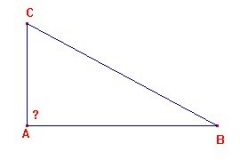
La quadrature du cercle est un des grands problèmes de géométrie de l’antiquité et l’est resté pendant longtemps. Il consiste à construire à la règle et au compas un carré de même aire qu’un disque de rayon donné, ce qui revient à construire le nombre (plus exactement le rapport) égal à la racine carrée de π. Si on prend 1 comme rayon du disque, l’aire est égale à π. Il faut donc trouver x le côté du carré tel que x² = π

Il fallut attendre la fin du XIXème siècle pour que Lindemann démontre que π est un nombre transcendant (c’est-à-dire qu’il n’est solution d’aucune équation à coefficients rationnels), ce qui prouve que π n’est pas constructible à la règle et au compas. En effet, si π était un nombre algébrique , il s’écrirait sous la forme d’une racine, et une racine est constructible à la règle et au compas (une racine carrée est constructible à la règle et au compas en utilisant des triangles rectangles)

Ce problème a laissé une trace derrière lui : l’expression ” résoudre la quadrature du cercle” est devenue synonyme de réaliser l’impossible.

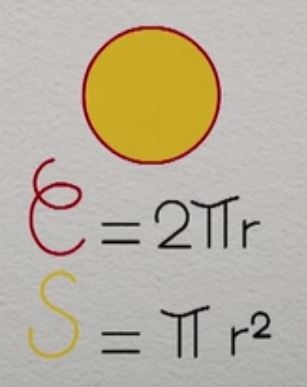
Pour le commun des mortels …Tout le monde (enfin, … en principe !) connaît la formule qui donne le périmètre d’un cercle à partir de son diamètre ou de son rayon et du nombre π qui vaut quelque chose comme 3,1415926535… :

soit Périmètre du cercle = π x diamètre
et
soit Périmètre du cercle = π x 2 x rayon

Que l’on écrit 2π x rayon

D’où la définition classique de π qui est :

π (pi) est le rapport constant entre la longueur d’un cercle (le périmètre du cercle) et son diamètre (le double de son rayon) π = P/d.
ou encore π = P/2r
Ou bien encore, à partir de la formule permettant de calculer l’aire (la “surface”) d’un disque (le disque est la surface comprise à l’intérieur du cercle) à partir de son rayon : Aire d’un disque A = π x (rayon du cercle)²

soit A = πr²
On obtient la définition suivante de π (qui est équivalente à la précédente) :

π (pi) est le rapport constant entre l’aire d’un disque et le carré de son rayon π = A/r²

Pour le mathématicien ?… Alors là vous allez rire !

La définition n’est pas la même.

La définition donnée précédemment à l’aide du périmètre du cercle ou de l’aire du disque est ennuyeuse pour le mathématicien (qui est très joueur en réalité) car elle suppose que l’espace dans lequel on se place soit euclidien pour que le rapport “périmètre du cercle / diamètre” soit constant et indépendant du cercle choisi (ce qui n’est pas vrai lorsqu’on trace des cercles sur une sphère, par exemple) et également qu’une théorie de l’intégration soit développée sur cet espace pour pouvoir calculer le périmètre du cercle ou l’aire du disque.

Ça a l’air compliqué non ? Ça l’est un peu j’avoue!

Aussi les mathématiciens préfèrent-ils une définition basée sur l’analyse.

Évidemment, elle est équivalente à la définition précédente et on obtient toujours le même nombre π ! Encore heureux.

 

Voici quelques étrangetés trouvées dans les décimales de π ; on se gardera bien de les prendre au sérieux.

• 1+4+1+5+9+2+6+5+3+5+8+9+7+9+3+2+3+8+4+6 = 100
• Le «0» n’apparaît la première fois qu’en position 32 après la virgule, alors que tous les autres chiffres sont déjà représentés au moins une fois dans les 13 premières décimales. Pourquoi ce retard du «0» ?
• Les décimales de π à partir de la 762e sont 999999. Qu’il y ait six «9» consécutifs quelque part dans le premier million de décimales de π ne serait pas étonnant, mais que cela se produise avant la millième décimale, n’est-ce pas troublant?
• En additionnant les 144 premières décimales de π, on trouve 666. Faut-il en conclure que π est satanique?
• Parmi les 1 000 premiers entiers obtenus en prenant les décimales de π dans l’ordre 3, 31, 314, 3 141, 31 415, …, seuls quatre sont des nombres premiers. N’est-ce pas vraiment très peu?
• Parmi les 400 premières décimales de π, il n’y a que 24 «7», ce qui est peu par rapport aux 40 «7» attendus.
• Le groupe de trois décimales qui se termine à la position 315 est 315, et celui qui se termine à la position 360 est 360… Mystère !
• (π4 + π5)1/6 = 2,718281809, soit la constante népérienne e jusqu’à la septième décimale !

 

Et voici ci-dessous, après calcul, les 10 000 premières décimales de Pi :

Chaque paragraphe contient 10 lignes, et chaque ligne est composée de 100 décimales.

Chaque paragraphe contient donc 1000 décimales, et il y a 10 paragraphes en tout soit au total 10 000 décimales.

Vous cherchez la 2637ème décimale ? C’est facile : il s’agit du 37ème chiffre de la 6ème ligne du 2ème paragraphe.

Autre exemple : où se trouve la 7518ème décimale ?

• 7000 –> dans le 7 ème paragraphe
• 500 –> sur la 5 ème ligne
• 18 –> c’est le 18 ème chiffre Et c’est le chiffre 5 !

Aucune régularité ou périodicité n’a jamais été constatée dans les décimales de Pi. Cela signifie qu’une suite quelconque de chiffres a de grande chance de se trouver dans la suite des décimales de Pi. Par exemple, votre date de naissance, exprimée sous la forme d’une suite de 6 chiffres JJMMAA se trouve-t-elle dans ces 10 000 premières décimales de Pi ?

Vous pouvez aussi y rechercher toute autre suite de chiffres vous caractérisant, comme par exemple votre numéro de sécurité sociale ou votre numéro de téléphone. Bonne recherche !!

Π = 3,
1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273
7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094
3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912
9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132
0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235
4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859
5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303
5982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989

3809525720106548586327886593615338182796823030195203530185296899577362259941389124972177528347913151
5574857242454150695950829533116861727855889075098381754637464939319255060400927701671139009848824012
8583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912
9331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279
6782354781636009341721641219924586315030286182974555706749838505494588586926995690927210797509302955
3211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000
8164706001614524919217321721477235014144197356854816136115735255213347574184946843852332390739414333
4547762416862518983569485562099219222184272550254256887671790494601653466804988627232791786085784383
8279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863
0674427862203919494504712371378696095636437191728746776465757396241389086583264599581339047802759009

9465764078951269468398352595709825822620522489407726719478268482601476990902640136394437455305068203
4962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382
6868386894277415599185592524595395943104997252468084598727364469584865383673622262609912460805124388
4390451244136549762780797715691435997700129616089441694868555848406353422072225828488648158456028506
0168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125
1507606947945109659609402522887971089314566913686722874894056010150330861792868092087476091782493858
9009714909675985261365549781893129784821682998948722658804857564014270477555132379641451523746234364
5428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344
0374200731057853906219838744780847848968332144571386875194350643021845319104848100537061468067491927
8191197939952061419663428754440643745123718192179998391015919561814675142691239748940907186494231961

 

 

5679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215
0306803844773454920260541466592520149744285073251866600213243408819071048633173464965145390579626856
1005508106658796998163574736384052571459102897064140110971206280439039759515677157700420337869936007
2305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116
7229109816909152801735067127485832228718352093539657251210835791513698820914442100675103346711031412
6711136990865851639831501970165151168517143765761835155650884909989859982387345528331635507647918535
8932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923
2332609729971208443357326548938239119325974636673058360414281388303203824903758985243744170291327656
1809377344403070746921120191302033038019762110110044929321516084244485963766983895228684783123552658
2131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396

6655730925471105578537634668206531098965269186205647693125705863566201855810072936065987648611791045
3348850346113657686753249441668039626579787718556084552965412665408530614344431858676975145661406800
7002378776591344017127494704205622305389945613140711270004078547332699390814546646458807972708266830
6343285878569830523580893306575740679545716377525420211495576158140025012622859413021647155097925923
0990796547376125517656751357517829666454779174501129961489030463994713296210734043751895735961458901
9389713111790429782856475032031986915140287080859904801094121472213179476477726224142548545403321571
8530614228813758504306332175182979866223717215916077166925474873898665494945011465406284336639379003
9769265672146385306736096571209180763832716641627488880078692560290228472104031721186082041900042296
6171196377921337575114959501566049631862947265473642523081770367515906735023507283540567040386743513
6222247715891504953098444893330963408780769325993978054193414473774418426312986080998886874132604721

5695162396586457302163159819319516735381297416772947867242292465436680098067692823828068996400482435
4037014163149658979409243237896907069779422362508221688957383798623001593776471651228935786015881617
5578297352334460428151262720373431465319777741603199066554187639792933441952154134189948544473456738
3162499341913181480927777103863877343177207545654532207770921201905166096280490926360197598828161332
3166636528619326686336062735676303544776280350450777235547105859548702790814356240145171806246436267
9456127531813407833033625423278394497538243720583531147711992606381334677687969597030983391307710987
0408591337464144282277263465947047458784778720192771528073176790770715721344473060570073349243693113
8350493163128404251219256517980694113528013147013047816437885185290928545201165839341965621349143415
9562586586557055269049652098580338507224264829397285847831630577775606888764462482468579260395352773
4803048029005876075825104747091643961362676044925627420420832085661190625454337213153595845068772460

2901618766795240616342522577195429162991930645537799140373404328752628889639958794757291746426357455
2540790914513571113694109119393251910760208252026187985318877058429725916778131496990090192116971737
2784768472686084900337702424291651300500516832336435038951702989392233451722013812806965011784408745
1960121228599371623130171144484640903890644954440061986907548516026327505298349187407866808818338510
2283345085048608250393021332197155184306354550076682829493041377655279397517546139539846833936383047
4611996653858153842056853386218672523340283087112328278921250771262946322956398989893582116745627010
2183564622013496715188190973038119800497340723961036854066431939509790190699639552453005450580685501
9567302292191393391856803449039820595510022635353619204199474553859381023439554495977837790237421617
2711172364343543947822181852862408514006660443325888569867054315470696574745855033232334210730154594
0516553790686627333799585115625784322988273723198987571415957811196358330059408730681216028764962867

4460477464915995054973742562690104903778198683593814657412680492564879855614537234786733039046883834
3634655379498641927056387293174872332083760112302991136793862708943879936201629515413371424892830722
0126901475466847653576164773794675200490757155527819653621323926406160136358155907422020203187277605
2772190055614842555187925303435139844253223415762336106425063904975008656271095359194658975141310348
2276930624743536325691607815478181152843667957061108615331504452127473924544945423682886061340841486
3776700961207151249140430272538607648236341433462351897576645216413767969031495019108575984423919862
9164219399490723623464684411739403265918404437805133389452574239950829659122850855582157250310712570
1266830240292952522011872676756220415420516184163484756516999811614101002996078386909291603028840026
9104140792886215078424516709087000699282120660418371806535567252532567532861291042487761825829765157
9598470356222629348600341587229805349896502262917487882027342092222453398562647669149055628425039127

5771028402799806636582548892648802545661017296702664076559042909945681506526530537182941270336931378
5178609040708667114965583434347693385781711386455873678123014587687126603489139095620099393610310291
6161528813843790990423174733639480457593149314052976347574811935670911013775172100803155902485309066
9203767192203322909433467685142214477379393751703443661991040337511173547191855046449026365512816228
8244625759163380391072253837421821408835086573917715096828874782656995995744906617583441375223970968
3408005355984917541738188399944697486762655165827658483588453142775687900290951702835297163445621296
4043523117600665101241200659755851276178583829204197484423608007193045761893234922927965019875187212
7267507981255470958904556357921221033346697499235630254947802490114195212382815309114079073860251522
7429958180724716259166854513331239480494707911915326734302824418604142636395480004480026704962482017
9289647669758318327131425170296923488962766844032326092752496035799646925650493681836090032380929345

 

 

9588970695365349406034021665443755890045632882250545255640564482465151875471196218443965825337543885
6909411303150952617937800297412076651479394259029896959469955657612186561967337862362561252163208628
6922210327488921865436480229678070576561514463204692790682120738837781423356282360896320806822246801
2248261177185896381409183903673672220888321513755600372798394004152970028783076670944474560134556417
2543709069793961225714298946715435784687886144458123145935719849225284716050492212424701412147805734
5510500801908699603302763478708108175450119307141223390866393833952942578690507643100638351983438934
1596131854347546495569781038293097164651438407007073604112373599843452251610507027056235266012764848
3084076118301305279320542746286540360367453286510570658748822569815793678976697422057505968344086973
5020141020672358502007245225632651341055924019027421624843914035998953539459094407046912091409387001
2645600162374288021092764579310657922955249887275846101264836999892256959688159205600101655256375678

Le nombre pi est partout !