Harris' blog

Archive pour la catégorie ‘Mathématiques’

Voici une belle réalité mathématique :

A la Question : Combien de fois peut-on soustraire 7 de 83 et combien reste-t-il ?
on est en droit de répondre : autant de fois que l’on veut et il reste 76 à chaque fois. Qu’en pensez-vous ?

Histoire vraie !

J’ai tenté d’expliquer dernièrement les limites des fonctions à une blonde (ou, si vous préférez, à une élève ayant, comme on dit, des “difficultés de compréhension” certaines). Je résous avec elle l’exercice suivant qui consiste à calculer la limite de la fonction 1/x-8 lorsque x tend vers 8 et lui démontre que :

A la fin de l’exercice, je lui ai demandé si elle avait tout compris :

“Oh oui, Harris ! J’ai tout compris!”

N’y croyant qu’à moitié, je lui pose l’exercice suivant.

Déterminer la limite de la fonction 1/x-5 lorsque x tend vers 5.

Voici sa réponse :

Comme on le dit souvent, il n’y a pas de mauvais élèves, seulement de mauvais professeurs… Mais là, quand même !

 

Quelques images récoltées ici et là sur le net et qui associent l’humour et l’amour avec les mathématiques !

 

 

Le zéro n’est pas rien, l’infini est plusieurs,  Pi n’a pas l’air naturel…

Les nombres nous en font voir de toutes les grandeurs ! Irrationnels, imaginaires ou transcendants… Les mathématiciens ne cessent de découvrir des nombres aux propriétés étranges.

Et pourtant, quoi de plus ordinaire que les nombres ?

Ce n’est pas pour rien qu’on les qualifie de naturels !

Mais les mathématiciens ne se contentent pas de les utiliser pour compter : ils démontrent, imaginent, conceptualisent. Regroupant les nombres en fonction de leurs propriétés, les pairs, les impairs, les premiers etc. Ils construisent des structures dans lesquelles effectuer des calculs.

Après une évolution de plusieurs millénaires, ils ont abouti à des familles de plus en plus riches, des structures mathématiques de plus en plus éloignées de la réalité tangible ou habituelle.

Jusqu’à décrire des nombres complexes qui associent une partie réelle à une partie imaginaire ! Vaste programme.

“Les nombres recouvrent tous les possibles ; ce sont en quelque sorte des modèles d’univers qu’il s’agit de décoder”, se passionne le mathématicien Canadien Simon Plouffe.

La scansion de 1, 2, 3, 4, 5, 6… a rythmé nos années de maternelle. Le nombre de crayons de couleurs dans une trousse, le nombre de pages d’un livre etc.

Il s’agit du début de l’ensemble des entiers naturels, les entiers positifs, noté N. De l’Italien : Naturale

On dispose de 10 chiffres pour écrire les nombres entiers. cette technique de numérotation s’appelle la numération en base dix. Elle obéit à quelques règles simples :

• le premier chiffre à droite représente le chiffre des unités du premier ordre.
• dans cette écriture, chaque chiffre représente 10 fois moins que celui qui est à gauche.
• le chiffre 0 tient la place des ordres manquant.

Attention à ne pas confondre “nombre” et “chiffre” ! 547 est un nombre écrit avec les chiffres 4,5,7. C’est la même nuance qu’il y a entre “mot” et “lettre”.

De nos jours, la base de dix est la plus répandue. on utilise cependant d’autres bases comme la base soixante pour les heures, minutes, secondes ainsi que les bases deux, huit et seize en informatique.

Le premier choc vient à l’école élémentaire avec l’ensemble Q des rationnels, ces nombres qui s’écrivent comme un rapport de deux entiers – par exemple 1/5, 2/3 ou 3/7.

Leur développement décimal, c’est à-dire le nombre de chiffres après la virgule qu’ils comportent, peut être fini, on les appelle alors décimaux. Noté D

Ainsi 1/4 = 0,25, est un nombre décimal alors que 1/3 = 0,333333 … N’en est pas un, il ne finit jamais.

Deuxième choc avec les nombres négatifs :

Quand j’ôte trois oranges de deux oranges, il reste moins une orange !   (2 – 3 = -1)… On peut aussi imaginer monter deux marches et en descendre trois, ce qui revient à n’en descendre qu’une seule (-1) !

Concept tout sauf naturel, mais cela ne dérange nullement le mathématicien qui y voit un outil de calcul bien utile.

Toutefois, s’il est fait mention dès le VIe siècle en Inde, de négatifs, assimilés à des dettes, ils n’accéderont au statut de nombres à part entière qu’avec la construction de l’ensemble des entiers relatifs, regroupant les entiers positifs et négatifs, par Richard Dedekind (mathématicien allemand) à la fin du XIXe siècle.

Un ensemble noté Z. De l’allemand Zahlen : compter

Plus tard, au collège (mais historiquement dès l’Antiquité grecque), nous découvrons que certains nombres ne peuvent s’exprimer sous la forme d’un rationnel.

L’exemple le plus frappant est celui de la diagonale d’un carré dont le côté est égal à 1 : cette diagonale vaut √2, un nombre qui ne peut être écrit sous forme d’un quotient d’entiers. La démonstration par l’absurde est un petit jeu intellectuel que j’adore faire à mes élèves.

Et voilà comment les irrationnels entrent en scène. On utilise le terme « irrationnel » non pas parce que ces nombres manquent de logique, mais simplement parce qu’ils ne peuvent pas se représenter sous la forme d’un « ratio », une fraction de deux nombres entiers.

Munis des relatifs, des rationnels et des irrationnels, l’allemand Richard Dedekind et Georg Cantor (mathématicien Russe) formalisent à la fin du XIXè et au début du XXè siècle un grand ensemble, celui des réels (R).

Pourquoi “réels” ?

Parce qu’ils sont les plus proches de notre idée de la réalité.

Pensons à une droite graduée partant de moins l’infini à plus l’infini.

Sur cette droite, arrêtons-nous en différents endroits. A chaque arrêt, et à condition bien sûr d’imaginer que nous avons un instrument de mesure infiniment précis, nous pouvons marquer un point dont la distance au point 0 est un nombre réel. Où que nous soyons sur la droite, il existe un nombre, et c’est en ce sens qu’il est “réel”.

Malgré cela, les nombres réels défient eux aussi notre intuition, car ils possèdent une étrange propriété : on ne peut les dénombrer, les compter.

La notion de dénombrabilité a été introduite par Cantor, le magicien des nombres qui, dès 1874, a distingué deux sortes de nombres réels.

D’une part, les nombres algébriques, c’est-à-dire qui sont la solution d’une équation polynomiale à coefficient entier (comme 3x² + 5x – 1 = O ou x³ – 7 = O) ;

D’autre part, les nombres qui ne sont pas solution de telles équations, appelés transcendants.

Si Cantor montre que les nombres algébriques sont dénombrables (on peut les compter), il montre également que les nombres transcendants ne le sont pas.

Autrement dit, l’ensemble des nombres réels est une infinité non dénombrable, constituée en très grosse majorité de nombres transcendants, infinis, non dénombrables…

Bientôt quelques articles sur des nombres vedettes : Pi, racine de 2, le nombre d’or etc.

Les Mathématiques

Qu’est-ce que c’est ? & Pourquoi faire ?

---

«La science des mathématiques est l’expression de la beauté et de la justice. Et puisque que les mathématiques sont partout autour de nous, profitons du bonheur qu’elles nous apportent et rendons leur hommage en les étudiant avec respect et humilité.»

Harris Puisais, mathématicien et économiste français.

---

Le mot « mathématique » comme aussi celui de « philosophie » serait dû à Pythagore (VI siècle avant JC).

(Je me permets d’ouvrir une petite parenthèse concernant Pythagore. On a accordé énormément de découvertes scientifiques à cet homme sans jamais avoir été absolument certain qu’il en était à l’origine. En effet, aucun écrit précis ne permet de lui attribuer autant d’avancées mathématiques. Pas plus qu’on est certain de son physique puisque les statues de lui ou autres représentations ont été faites bien après sa mort. On connait son école, dont il est le fondateur, l’école pythagoricienne. Ecole ou secte ? Les pythagoriciens n’étaient pas férus de propreté parait-il. Pythagore disait pouvoir expliquer le cosmos au moyen de nombres: “Les nombres sont les causes et les principes de toutes les choses”, il avait même réussi à fabriquer une gamme de musique, la gamme Pythagoricienne qui s’exprime par des rapports de nombres entiers, puis il a tenté d’expliquer l’astronomie par les mêmes règles: la musique des sphères et enfin, il a voulu associer les 5 éléments, terre, air, eau, feu et un 5ème inconnu à 5 figures géométriques, des polyèdres réguliers. C’est lorsqu’il a étudié le carré de côté égal à 1 qu’il s’est rendu compte que la diagonale n’était pas un nombre entier… Ses théories étaient déjà mises à mal au tout commencement.).

Il provient du grec mat^hêma qui veut dire « science » dans l’optique de l’époque, c’est-à-dire « toute la connaissance ».

Mat^hêmatika en grec comme mathematica en latin sont des pluriels, c’est pourquoi on dit des mathématiques. Certains essaient de parler de la mathématique, pour montrer son unité, mais cela ne prend pas. Notons qu’en anglais on dit mathematics avec un s, mais que c’est un mot singulier…

L’usage de la lettre X remonte à René Descartes.

Mais l’idée de donner un nom à l’inconnue d’un problème est plus ancienne encore, puisqu’elle vient du mathématicien grec Diophante IIIe siècle, qui l’appelait « arithmos », le nombre.

Sur la tombe de Diophante on pouvait lire: Passant, c’est ici le tombeau de Diophante. C’est lui qui t’apprend le nombre d’années qu’il a vécu. Sa jeunesse en a occupé la sixième partie. Puis sa joue se couvrit d’un premier duvet pendant la douzième. Il passa encore le septième de sa vie avant de prendre une épouse et, cinq ans plus tard, il eut un bel enfant qui après avoir atteint la moitié de l’âge final de son père, périt d’une mort malheureuse. Son père lui survécut quatre années. De tout ceci, déduis son âge.

Je vous laisse réfléchir un peu… c’est bon ? Oui en effet, il avait 84 ans !

Plus tard, le mathématicien perse Al-Kwarizmi, IXe siècle, la nomma « shay », la chose en arabe. Cette pratique parvint en France grâce aux Espagnols, qui transcrivaient ce mot en « xay ». Descartes simplifia en ne gardant que l’initiale, d’où « X ».

Son usage s’étendit ensuite, en particulier au monde judiciaire.

En mathématiques, la lettre « X » porte le nom d’inconnue quand il s’agit de résoudre une équation, d’indéterminée s’il est question de polynômes et de variable dans le cadre des fonctions. Un triple statut qui est parfois source de confusions.

Des outils pour une infinité d’applications

Les mathématiques possèdent plusieurs branches telles que :

• l’arithmétique,
• l’algèbre,
• l’analyse,
• la géométrie,
• la topologie,
• la logique mathématique, la statistique, les probabilités, etc.

Il existe également une certaine séparation entre les mathématiques pures et les mathématiques appliquées.

C’est un ensemble de connaissances abstraites résultant de raisonnements logiques appliqués à des objets divers tels que les nombres, les figures, les structures et les transformations. Les mathématiques sont aussi le domaine de recherche développant ces connaissances, ainsi que la discipline qui les enseigne.

Elles se distinguent des autres sciences par un rapport particulier au réel car l’observation et l’expérience ne s’y portent pas sur des objets physiques. Elles sont de nature entièrement intellectuelle, fondées sur des axiomes déclarés vrais ou sur des postulats provisoirement admis. Ces axiomes en constituent les fondements et ne dépendent donc d’aucune autre proposition. Un énoncé mathématique – dénommé généralement, après être validé, théorème, proposition, lemme, fait, scholie ou corollaire – est considéré comme valide lorsque le discours formel qui établit sa vérité respecte une certaine structure rationnelle appelée démonstration, ou raisonnement logico-déductif.

Un énoncé présenté comme plausible, mais qui n’a pas encore été établi comme vrai (“démontré”, en langage utilisé par les mathématiciens), s’appelle une conjecture.

Bien que les résultats mathématiques soient des vérités purement formelles, ils trouvent cependant des applications dans les autres sciences et dans différents domaines de la technique. C’est ainsi qu’Eugène Wigner parle de « la déraisonnable efficacité des mathématiques dans les sciences de la nature »

Comme beaucoup de monde sur cette planète vous vous posez la question : mais à quoi ça sert les maths?

La réponse est à la fois facile : les maths, ça sert partout, et difficile, car il n’est pas évident de donner des exemples qui se situent au niveau du commun des mortels.

En fait, des maths beaucoup plus élaborées sont présentes, mais de manière cachée, dans la vie de tous les jours. Lorsque vous regardez les prévisions météo à la télé, elles sont derrière, avec aussi beaucoup de physique et d’informatique, dans les modèles qu’il a fallu mettre en place pour comprendre le comportement de l’atmosphère.

L’outil principal dans tout cela est la notion de fonction.

Tout le monde a au moins une perception intuitive de ce que l’on appelle une fonction (numérique) : on se donne une suite de règles — une recette, ou une transformation — permettant de fabriquer un deuxième nombre, Y, à partir d’un premier x.

x peut être un entier, un réel, un complexe, un quaternion, en principe tout est envisageable, rien n’est interdit ; la recette, ce peut être par exemple d’élever x au carré et de lui ajouter 3, obtenant ainsi Y = x² + 3.

Techniquement, on note x → Y = f(x), f désignant la recette.

Ou encore : x → Y = f(x) = x² + 3.

Cela fait, une question vient immédiatement à l’esprit.

Il est sûr que quand x varie, Y — donc f(x) — varie aussi.

Dès lors, quand x varie gentiment autour d’une valeur fixe x₀, sans « sauter », la fonction f fait-elle de même ?

Si oui, on dit que f est continue en x₀. Techniquement, cela s’exprime en invoquant un processus de limite, difficile à bien comprendre, mais d’une importance capitale. Intuitivement, la continuité signifie que quand on s’approche de x₀ (supposé pour simplifier être un nombre réel), on trouve la même valeur pour f que l’on arrive en x₀ par au-dessous (par valeurs inférieures) ou par au-dessus (par valeurs supérieures).

Une autre notion essentielle est celle de dérivée, survenant naturellement quand on se demande comment varie Y (vite, pas vite ?) quand x varie. Pour cela, on fabrique le rapport entre l’accroissement ΔY et l’accroissement Δx au voisinage d’une valeur fixe x₀ : si ce rapport a une grande valeur, qu’elle soit absolue ou non, cela veut dire que la fonction varie vite, s’il est petit, la fonction varie lentement. Ensuite, on examine ce qui se passe quand Δx devient de plus en plus petit. Poussant les choses à l’extrême, on passe à la limite au sens du mathématicien et alors, de deux choses l’une :

Ou bien la limite existe — on dit alors que la fonction est dérivable en x₀, et on note f'(x₀) la valeur de la limite, ou elle n’existe pas.

Dans les cas ordinaires (les « bonnes » fonctions), la dérivée existe sauf peut-être pour quelques valeurs de x, le « quelques » pouvant d’ailleurs être très grand, voire aussi grand que le nombre de nombres entiers, N; on a longtemps cru que ce dernier cas, pour une fonction continue, était le pire possible, à la limite une invention du diable !

Vers 1870, Bolzano, Weierstrass et du Bois-Reymond ont exhibé des exemples de fonctions continues partout, mais n’ayant nulle part de dérivée, provoquant l’ire de Charles Hermite : « Je me détourne avec effroi et horreur de cette plaie lamentable des fonctions continues qui n’ont point de dérivées », et la perplexité de Poincaré : « Autrefois, quand on inventait une fonction nouvelle, c’était en vue de quelque but pratique ; aujourd’hui, on les invente tout exprès pour mettre en défaut les raisonnements de nos pères, et on n’en tirera jamais que cela. »

Il arrive aux plus grands génies de se tromper. Bien sûr, il n’y a rien de coupable dans l’imagination de Bolzano et ses compères, car les grandes découvertes mathématiques résultent souvent de prémisses qui semblent extravagantes pour le béotien, et parfois même monstrueuses pour les initiés. Et puis, on peut aussi se dire que si les mathématiciens sont en droit de soudainement sortir des sentiers battus, leurs apparentes divagations ne servent pas à grand-chose en pratique, et que ce n’est pas cela qui va inverser le champ magnétique terrestre ou faire sortir aujourd’hui de l’utopie les applications civiles de la fusion nucléaire.

Jean Perrin, prix Nobel de physique 1926, a apporté la première preuve de l’existence des atomes en utilisant une formule d’Einstein issue de ses travaux sur le mouvement brownien. Il a fait le lien entre les trajectoires de particules effectuant un tel mouvement et les fonctions non dérivables découvertes au XIX^e siècle.

Il aura fallu le génie de Jean Perrin, vers 1905 (année bénie des dieux) pour réaliser que ces monstres existent (presque) dans la nature. Étudiant le mouvement aléatoire de petites particules dans un fluide (mouvement brownien) à l’aide d’un simple microscope optique, Perrin écrit — la citation intégrale est de rigueur — : « On ne peut non plus fixer une tangente, même de façon approchée, à aucun point de la trajectoire, (En effet, pour construire une trajectoire, il faut définir avec une précision totale et au même instant, un point (qui donne la position) et en ce point une tangente (qui donne la vitesse)) et c’est un cas où il est vraiment naturel de penser à ces fonctions continues sans dérivées que les mathématiciens ont imaginées, et que l’on regarderait à tort comme des curiosités mathématiques, puisque la nature les suggère aussi bien que les fonctions à dérivées. »

Ainsi, les monstres imaginés par Bolzano existent dans la nature ? Presque, car ici intervient une subtilité à propos de laquelle il arrive que (certains) mathématiciens et (certains) physiciens s’empoignent comme des chiffonniers. La subtilité est que le mathématicien peut passer à la limite avec son crayon sur son papier, mais que le physicien, lui, ne peut jamais le faire, car la nature, souveraine, a ses règles et ses échelles dont nul ne peut disposer à sa guise.

Quand Perrin traduisait en ses termes sa fulgurante intuition, il savait bien que, strictement, ce n’était pas tout à fait vrai : pour fabriquer la tangente (donc la dérivée), il faut passer à la limite d’accroissements nuls (pour la position et l’intervalle de temps). Or lui, Jean Perrin, ardent défenseur de l’atomisme envers et contre tous, savait bien qu’il y a forcément une échelle de longueur minimale en dessous de laquelle le physicien est aveugle au sens où ce que lui disent ses yeux à plus grande échelle ne doit pas être extrapolé vers l’infiniment petit (tiens, tiens, comme en mécanique quantique ?).

Le physicien doit croire ce qu’il voit, avec ses yeux, avec ses appareils ou à travers les théories qui expliquent l’expérience, pas plus.

Cet exemple met en lumière ce qu’il ne faut pas considérer comme une ligne de fracture entre l’univers des mathématiciens et celui des physiciens — tout juste une ligne de démarcation, et encore est-elle floue —, gardant en tête que, finalement, le zéro et l’infini des premiers sont toujours à relativiser pour les seconds, ces derniers devant toujours se référer aux échelles physiques du problème qu’ils analysent. Pour qui fait de la spectroscopie atomique, la distance Terre-Lune, c’est vraiment l’infini, alors que pour le cosmologiste, c’est un « infiniment petit » ; pour qui se demande comment les atomes s’assemblent pour former des molécules, le noyau atomique est un point de rayon nul (et sans structure, comme tout bon point) alors que pour l’expert en gluons et quarks, le noyau, c’est un peu comme une galaxie.

L’importance des échelles se mesure aussi à propos de l’opération, à priori banale, en tout cas élémentaire, consistant à vouloir tracer le graphe des fonctions de Bolzano et Weierstrass. Le physicien est tenté de le faire, mais il s’aperçoit vite qu’il ne peut pas (ni lui, ni personne) : pour représenter graphiquement cette fonction, il faudrait un crayon dessinant un trait infiniment fin, et cela n’existe pas.

Alors il se contentera de dessiner, dans un premier temps, quelque chose comme ce qui est représenté sur la figure ci-dessous (extraite de l’ouvrage Des mathématiques pour les sciences, Claude Aslangul, De Boeck, Bruxelles, 2011). Ensuite, prenant un crayon beaucoup plus fin, il pourra faire le dessin de droite ; il pourrait recommencer, mais de toute façon, il ne pourra jamais faire beaucoup mieux, même avec un crayon ayant la pointe d’un quark. En tout cas, les dessins lui donnent une bonne idée du caractère monstrueux des objets qu’il manipule — et notamment de leur invariance d’échelle —, c’est déjà pas mal.

Représentation graphique d’une approximation de la fonction de Weierstrass.

Un zoom sur un intervalle ([0; 0,0001], par exemple) produit un graphe ayant grosso modo la même allure (à droite). © Claude Aslangul

Le mathématicien, lui, dira que le graphe est impossible à tracer, et il a raison. Mais est-ce vraiment une cause de divorce ?

Dans beaucoup d’autres domaines, notamment tout ce qui concerne la génétique (par exemple les tests ADN, dont on parle beaucoup dans les affaires policières) interviennent les statistiques.

En fait, dans le moindre des objets que vous manipulez dans la vie courante, il y a des maths. Lorsque, dans un magasin, le lecteur optique n’arrive pas à lire un code-barre et que la caissière doit le taper, les derniers chiffres sont ce qu’on appelle une clé, la machine les trouve à partir des autres par un petit calcul, et cela permet de détecter si la caissière se trompe. C’est aussi le cas pour les numéros de sécurité sociale.

Même si certaines des maths actuelles semblent être dépourvues d’applications, rien ne dit qu’elles n’en auront pas demain.

Voici deux exemples en ce sens.

Le premier concerne ce qu’on appelle les coniques.

Ce sont des courbes (ellipses, paraboles, hyperboles) que vous avez peut-être déjà vues et que les anciens Grecs étudiaient pour leurs propriétés géométriques (voir figure ci-dessous).

A l’époque, elles n’avaient pas d’applications. Ce n’est qu’au XVIIème siècle que Kepler un éminent astronome, s’est aperçu que les trajectoires des planètes étaient justement des ellipses. De nos jours, ces courbes sont utiles dès qu’on envoie un satellite (et vous savez combien c’est important pour le téléphone, la télévision, le GPS, etc.)

L’autre exemple concerne l’arithmétique.

Si on avait demandé, dans les années 1970, à quoi servaient les nombres premiers dans la vie courante, on aurait répondu sans hésiter, à rien, et qu’en tout cas ils ne servaient pas à faire la bombe atomique…

Quarante ans plus tard, il faut reconnaître que l’on aurait dit une bêtise, puisque les nombres premiers, avec le code RSA (Le chiffrement RSA (nommé par les initiales de ses trois inventeurs) est un algorithme de cryptographie asymétrique, très utilisé dans le commerce électronique, et plus généralement pour échanger des données confidentielles sur Internet. Cet algorithme a été décrit en 1977 par Ronald Rivest, Adi Shamir et Leonard Adleman.

RSA a été breveté par le Massachusetts Institute of Technology (MIT) en 1983 aux États-Unis. Les maths jouent maintenant un rôle de premier plan dans presque tous les secteurs de la communication, de la finance, etc. et que parmi les plus grands utilisateurs se trouvent justement … les militaires.

Météo, informatique, trafic routier: les maths sont partout autour de nous…

Pour beaucoup, les maths sont aussi obscures qu’un trou noir dans le Cosmos, mais paradoxalement, nous y faisons appel tous les jours. Au-delà d’une bonne vieille règle de trois pour équilibrer une recette, ou d’une équation pour savoir combien dépenser pendant les soldes, voici plusieurs exemples de cas concrets où les maths nous rendent quelques services. Sans forcément qu’on s’en rende compte.

Je parlais à l’instant de la finance, mon père faisait partie de l’équipe de mathématiciens et d’économistes qui ont mis au point la formule du CAC 40 (figure ci-dessous)

CAc = (initialement qui signifiait « Compagnie des agents de change » et désormais devenu : cotation assistée en continu) est le principal indice boursier de la Bourse de Paris.

Créé avec 1 000 points de base au 31 décembre 1987 par la Compagnie des agents de change, l’indice CAC 40 est déterminé à partir des cours de quarante actions cotées en continu sur le premier marché parmi les cent sociétés dont les échanges sont les plus abondants sur Euronext Paris qui fait partie de Euronext, la première bourse européenne. Ces sociétés, représentatives des différentes branches d’activités, reflètent en principe la tendance globale de l’économie des grandes entreprises françaises et leur liste est revue régulièrement pour maintenir cette représentativité.

Les prévisions météo.

Derrière le sourire d’Evelyne Dhéliat se cache une batterie de calculs insoupçonnés. «Les prévisions sont le fruit de modèles très difficiles et extrêmement puissants», souligne Marc Peigné, mathématicien et président de la SMF, la société mathématique de France. Plusieurs branches des maths seraient utilisées en météorologie comme les probabilités, les équations à dérivées partielles et les statistiques. Mais aussi la mécanique des fluides, propre à la physique.

Les requêtes sur les moteurs de recherche.

Taper une occurrence dans Google pour obtenir une liste de résultats est également le fruit d’opérations mathématiques complexes. Anne De Bouard, directrice de recherche au CNRS, évoque le théorème de point fixe utilisé par le moteur de recherche. Google fait aussi appel à un intermédiaire entre informatique et mathématiques, l’algorithmique, qui se rapproche de l’algèbre.

Le cryptage des données bancaires.

Il s’agit du traitement de ce que les spécialistes appellent la gestion des flux. Les questions de cryptographie et de sécurisation des données nous échappent, mais feraient appel à des mathématiques très structurées, selon Peigné: «Si on ne veut pas que des codes de carte bleue soient interceptés, on fait indirectement appel à la théorie des nombres (les fameux nombres premiers indivisibles). On cherche les nombres premiers les plus importants. Cela permet d’affiner et renforcer encore la sécurité de ces codes», avance le mathématicien.

Rappelons brièvement l’utilité des clés dans le processus de cryptage/décryptage. Généralement un message secret est envoyé sous forme codée, une clé de conversion permettant de traduire le message codé en clair. Cette clé évite de devoir chiffrer et déchiffrer le message car l’émetteur et le destinataire disposent chacun d’une clé générant son propre système d’encryptage. Cette protection empêche même les concepteurs du programme d’encryptage de déchiffrer le message codé.

La sécurité d’un message codé dépend du nombre de clés. Un système à clé unique par exemple permet de “casser” un système, mais en général il va essayer systématiquement toutes les clés possibles sur le message à déchiffrer jusqu’à pouvoir le lire.

Certains systèmes comme la substitution mono alphabétique simple, dispose d’un nombre de clés gigantesque : 26! = 26 x 25 x 24 x 23 x 22…x 1 permutations possibles des lettres de l’alphabet, soit environ 4 x 10²⁶ possibilités.

Le succès est donc loin d’être garanti dans un temps relativement court. Pour remédier à ce problème on peut utiliser des variations de fréquence des lettres dans les différentes langues naturelles, ce qui permet d’aboutir à des systèmes de cryptage disposant d’un nombre de clés réduit mais qui s’avèrent souvent beaucoup plus sûrs.

Devant ce défi qui intéresse autant les majors de l’informatique que les services d’espionnage ou l’armée, des centaines de chercheurs aux quatre coins du monde se sont donnés pour objectif de construire le premier ordinateur quantique d’ici quelques années.

Certains très optimistes avancèrent même la date de 2020. Il est toutefois peu probable que nous verrons des ordinateurs quantiques au quotidien avant plusieurs décennies… Quoiqu’il en soit, la compétition est ouverte, avis aux chercheurs !

La régulation du trafic routier.

Non, Bison Futé ne prédit pas les embouteillages en tendant une narine au vent. La régulation des vitesses sur les autoroutes, les annonces de bouchons, dépendent aussi des maths qui offrent des marges d’erreur de plus en plus fiables. Idem pour la gestion des flux ferroviaires. Derrière eux se cachent de puissants calculs de probabilités.

L’écoute de musique sur lecteur MP3.

Quand un son numérisé trouve sa place dans un boîtier miniature, le transfert s’effectue par un procédé mathématique complexe, appelé «traitement du signal» par les scientifiques. Anne De Bouard parle de «modélisation et compression du son à travers des algorithmes spécifiques.»

La conception automobile.

Désormais, aucune voiture ne sort de l’usine sans être passée par un processus de simulation mathématique poussé. L’aérodynamisme, la climatisation dans l’habitacle, les interférences électromagnétiques émanent d’équations qui échappent au commun des mortels.

Mais qui, au final, s’avèrent indispensable pour toute personne sortant de chez le concessionnaire.

La maîtrise des opérations est utile pour faire ses courses, qu’il faut savoir calculer des longueurs ou des aires lorsqu’on bricole et que la connaissance des pourcentages et de la proportionnalité peut servir pour calculer l’impôt qu’on devra payer ou les intérêts d’un prêt bancaire.

Vous vous en êtes sûrement aperçus au fil des années, le temps semble passer plus vite lorsque l’on vieillit.

C’est cette perception qui peut paraître abstraite que je vais essayer de démontrer, mathématiquement parlant. Ainsi on passera de l’abstrait au pseudo concret.

Le temps semble passer plus vite lorsque l’on vieillit. Et ceci a du sens : lorsque l’on a 10 ans, une année représente 10 % de notre vie, et semble vraiment une durée très longue. À 50 ans, une année ne représente plus que 2 % de notre vie, et peut sembler durer 5 fois moins longtemps.

C’est en faisant cette observation que l’on arrive à la conclusion que l’âge réel (AR) doit être corrigé par la durée apparente d’une année (notée DAA).

La durée apparente d’une année est inversement proportionnelle à l’âge réel de la personne (plus on est âgé, moins une année dure longtemps en apparence).

On obtient :

DAA = a/AR 

La constante de proportionnalité a est définie comme “l’âge auquel une année semble durer une année” et est fixée arbitrairement à 20 ans.

a = 20

On définit maintenant le concept de l’âge perçu (AP) comme l’intégrale du temps de la durée apparente d’une année de 1 à l’âge réel :

Maintenant, critiquons cette formule obtenue.

• Le choix de la constante a est totalement arbitraire. Il n’y a pas une justification rationnelle à sa valeur qui est fixée selon une simple perception tout à fait personnelle et subjective j’en conviens.
• L’intégrale semble incorrecte car sa borne inférieure a été fixée à 1 et non à 0 (ce qui correspondrait à la naissance). Un tel choix est justifié par le fait que le logarithme népérien ne pouvait pas être évalué en 0.

Tentons de redéfinir l’âge perçu. La perception habituelle du temps indique que l’âge réel (AR) est une fonction affine du temps.

AR = bt + c

D’ordinaire, les paramètres b et c valent respectivement 1 et 0. Cependant, chacun a un rôle à jouer dans la perception du temps.

• Le paramètre b indique la vitesse a laquelle la personne vieillit : certaines personnes restent des bébés toute leur vie tandis que d’autres sont déjà des papis à 20 ans.
• Le paramètre c est l’ordonnée à l’origine de la perception du temps. N’avez-vous jamais rencontré des parents fiers de leur enfant parce que celui-ci marchait plus tôt que la normale ? Ce jeune et talentueux chef d’entreprise ? Ces personnes ne sont pas brillantes, elles ont un paramètre c plus fort que les autres.

Il est clair qu’avec cette définition, l’âge réel (AR) d’une personne n’est pas proportionnel au temps. Pareil que précédemment, la durée apparente d’une année (DAA) n’est pas constante :

On peut transformer l’expression pour supprimer un paramètre et en faire apparaître deux nouveaux.

Les paramètres d=a/b et e=c/b seront alors les conditions aux limites.

Pour obtenir l’âge perçu, on travaille avec l’intégrale de la durée apparente d’une année. L’intégrale est évaluée en fonction du temps, et non en fonction de l’âge réel car l’âge réel est une fonction du temps.

La condition limite inférieure (t = 0) doit donner un âge perçu de 0 (AP = 0). Ainsi,     e = 1.

La condition limite supérieure est moins facile. On doit avoir à t = t max, AP = t. À la mort, l’âge perçu et l’âge réel sont de nouveaux égaux. Pour autant, personne ne connait avec certitude son espérance de vie. Si l’on considère une personne dont l’espérance de vie est de 80 ans (t = 80, AP = 80), on obtient :

Cette formule peut donc être utilisée pour calculer l’âge perçu et l’avancement de la vie en pourcentage associé :

Et en traçant un petit graphique :

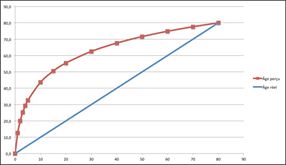
La vie est à moitié “terminée” à 10 ans et aux 3/4 à 30 ans. Il faut noter la rapide progression lors de l’enfance. Les grands changements arrivent pendant l’enfance : l’apprentissage de la parole, de la marche, de la lecture, des nombres… Des choses qui sont apprises au plus jeune âge et qui restent pour toute la vie.

 Conséquences

Les vacances d’été duraient une éternité lorsque j’étais tout petit ! Oui. Quand j’avais 6 ans, la durée apparente d’une année était environ de 3 ans. Ainsi, mes 2 mois de vacances d’été paraissaient en durer 6.

Maintenant que je suis plus vieux, je peux mieux discuter avec mes parents. Vrai. Plus je deviens vieux, moins la différence d’âge se fait sentir, puisque je me rapproche d’eux considérablement.

La vie commence à 65 ans. Des personnes proches de la retraite disent souvent ceci. C’est faux, à 65 ans, il ne reste plus que 5 % de votre âge perçu à vivre.

Votre temps est précieux…

Merci de m’avoir lu 🙂 et un grand merci à Antoine Augusti pour m’avoir aidé dans la rédaction de cet exposé totalement inutile mais qui m’a fait passer un peu de temps…

 

T. L. Freeman, Why it’s later than you think, J. Irr. Res., 1983.